Egy feladat és ami róla az eszembe jutott...
A 2019 évi Nemzetközi Magyar Matematikaverseny egyik, 9. osztályosoknak szóló feladatát Erdős Gábor (Batthyány Lajos Gimnázium, Nagykanizsa) javasolta. A feladatra matematika tanárok egy csoportja 20 elemi megoldást adott. A teljes anyag megtalálható a https://matek.fazekas.hu/ portálon a cikkek között, amit Erdős Gábor kollégám jegyez. Most ezek közül 7 megoldást mutatok. Mind a hét a maga nemében szép, vagy valami szép tulajdonságot használ. A megoldások közül az első három Erdős Gáboré; az utolsó négy megoldást én adtam.
A feladat
Az ![]() szabályos háromszög
szabályos háromszög ![]() oldalának felezőpontja
oldalának felezőpontja ![]() . A
. A ![]() szakasz azon belső pontja a
szakasz azon belső pontja a ![]() pont, amelyre az
pont, amelyre az ![]() szög 90 fokos. A
szög 90 fokos. A ![]() szakasz azon belső pontja az
szakasz azon belső pontja az ![]() pont, amelyre a
pont, amelyre a ![]() és a
és a ![]() szakaszok hossza egyenlő. Hány fokos az
szakaszok hossza egyenlő. Hány fokos az ![]() szög?
szög?
1. megoldás
Legyen a háromszög oldalának hossza 2 egység.
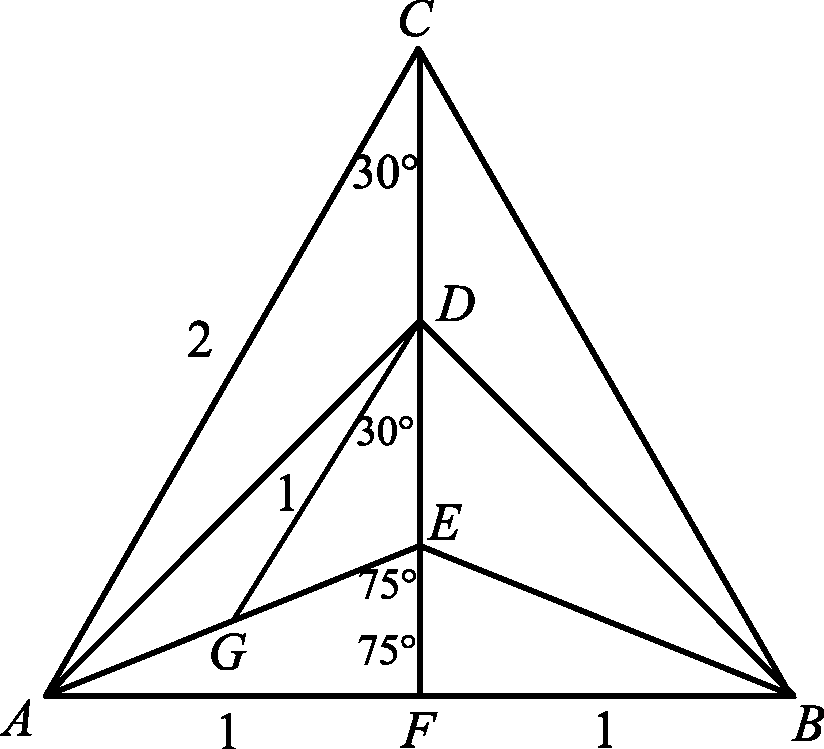
Legyen az ![]() szakasz felezőpontja
szakasz felezőpontja ![]() .
.
![]() középvonal az
középvonal az ![]() háromszögben, így
háromszögben, így
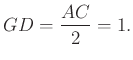
Az ![]() háromszög egyenlő szárú és derékszögű, így
háromszög egyenlő szárú és derékszögű, így
Az ![]() háromszög egyenlő szárú, mivel
háromszög egyenlő szárú, mivel
hiszen egyállású szögek, ezért
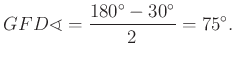
A Thalész-tétel megfordítása miatt az ![]() háromszög köré írt kör középpontja
háromszög köré írt kör középpontja ![]() , így az
, így az ![]() háromszög is egyenlő szárú, azaz
háromszög is egyenlő szárú, azaz
A kérdezett szög tehát:
2. megoldás
Legyen a háromszög oldala 2 egység. Használjuk az ábra jelöléseit.
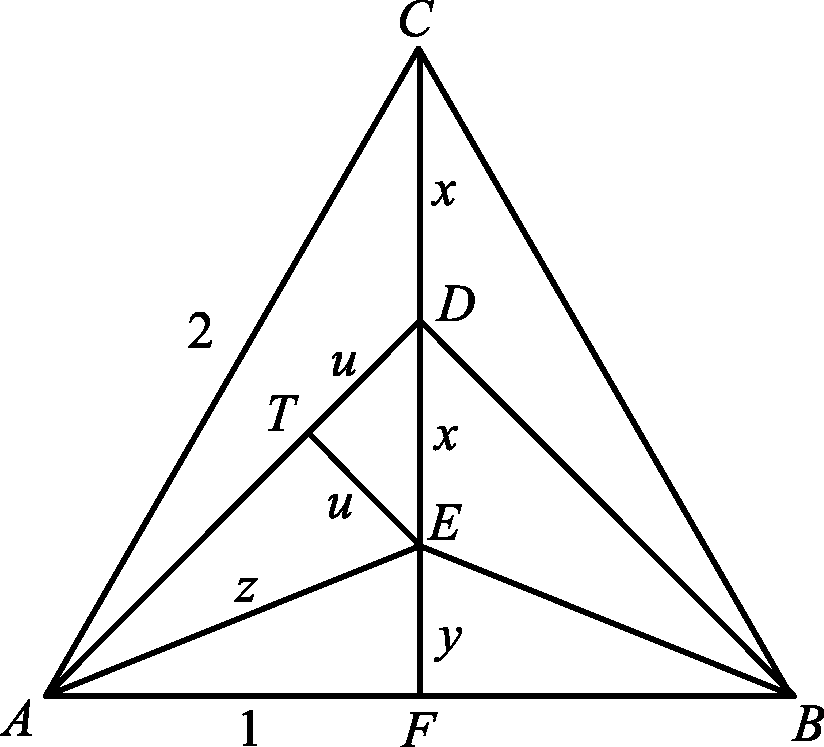
Az ![]() háromszögben a Pitagorasz-tétel miatt
háromszögben a Pitagorasz-tétel miatt
az ![]() háromszög egyenlő szárú, így
háromszög egyenlő szárú, így
ezért
és
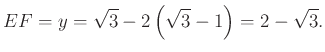
az ![]() háromszögben a Pitagorasz-tétel miatt
háromszögben a Pitagorasz-tétel miatt
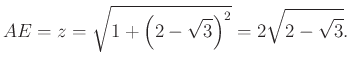
legyen az ![]() -ből az
-ből az ![]() -re bocsátott merőleges talppontja
-re bocsátott merőleges talppontja ![]() .
.
Az ![]() háromszögben a Pitagorasz-tétel miatt
háromszögben a Pitagorasz-tétel miatt
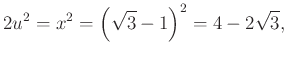
vagyis
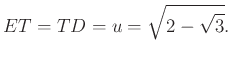
De akkor az ![]() derékszögű háromszögben
derékszögű háromszögben
ez tehát egy félszabályos háromszög, amiből következik, hogy
Ekkor viszont
így
A kérdezett szög tehát:
3. megoldás
Legyen a háromszög oldala 2 egység. Használjuk az ábra jelöléseit.
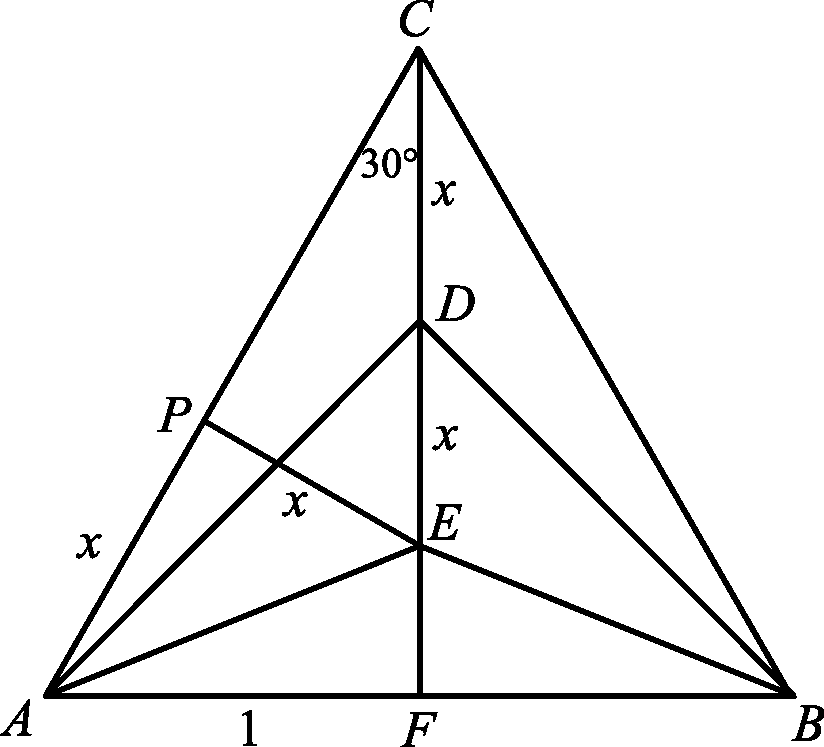
Az ![]() háromszögben a Pitagorasz-tétel miatt
háromszögben a Pitagorasz-tétel miatt
Az ![]() háromszög egyenlő szárú, így
háromszög egyenlő szárú, így
Legyen ![]() -ből az
-ből az ![]() -re bocsátott merőleges talppontja
-re bocsátott merőleges talppontja ![]() . Ekkor
. Ekkor ![]() félszabályos háromszög, így
félszabályos háromszög, így
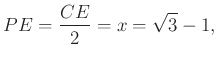
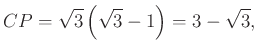
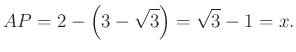
Azt kaptuk, hogy az ![]() derékszögű háromszögben
derékszögű háromszögben
tehát ez a háromszög egyenlő szárú is, ezért alapon fekvő szöge
Az ![]() háromszög
háromszög ![]() csúcsnál lévő külső szöge ezért
csúcsnál lévő külső szöge ezért
A kérdezett szög tehát:
4. megoldás
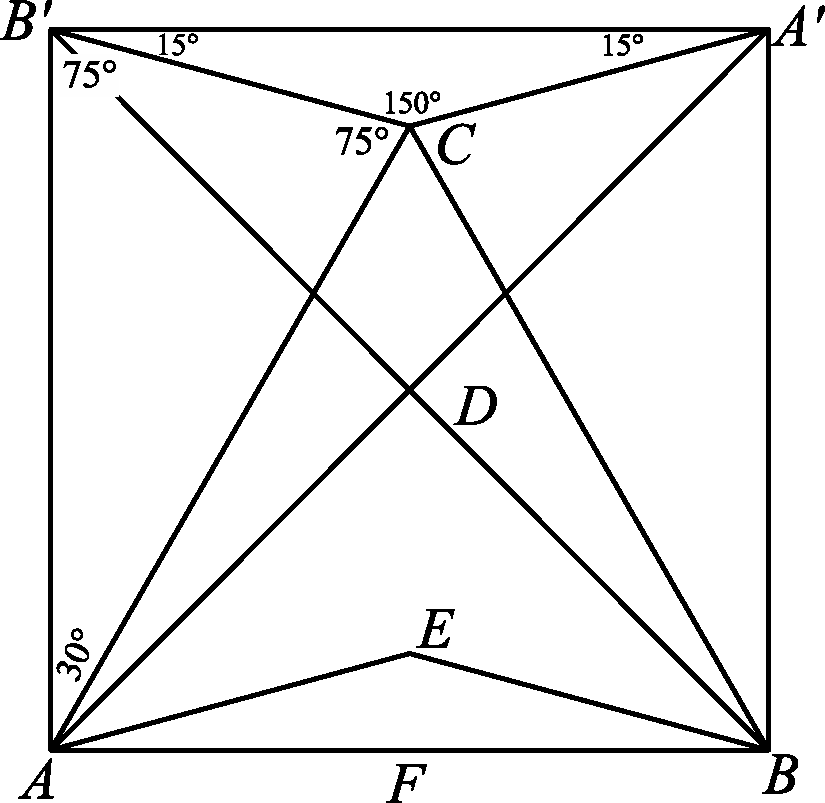
Tükrözzük az ![]() háromszöget a
háromszöget a ![]() pontra. Ekkor az
pontra. Ekkor az ![]() tükörképe
tükörképe ![]() .
.
Az így kapott ![]() négyszög egy négyzet, hiszen átlói merőlegesek és egyenlő hosszúak. A négyzet belsejében pedig az
négyszög egy négyzet, hiszen átlói merőlegesek és egyenlő hosszúak. A négyzet belsejében pedig az ![]() szabályos háromszög – ismert feladathoz jutottunk!
szabályos háromszög – ismert feladathoz jutottunk!
továbbá az ![]() háromszög egyenlő szárú, így
háromszög egyenlő szárú, így
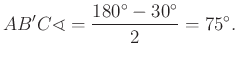
de akkor
Szimmetria-okokból a ![]() háromszög egyenlő szárú, így
háromszög egyenlő szárú, így
ezért
A keresett szög ennek a szögnek a tükörképe a ![]() pontra nézve, így
pontra nézve, így
5. megoldás
Legyen a háromszög oldala 2 egység. Használjuk az ábra jelöléseit.
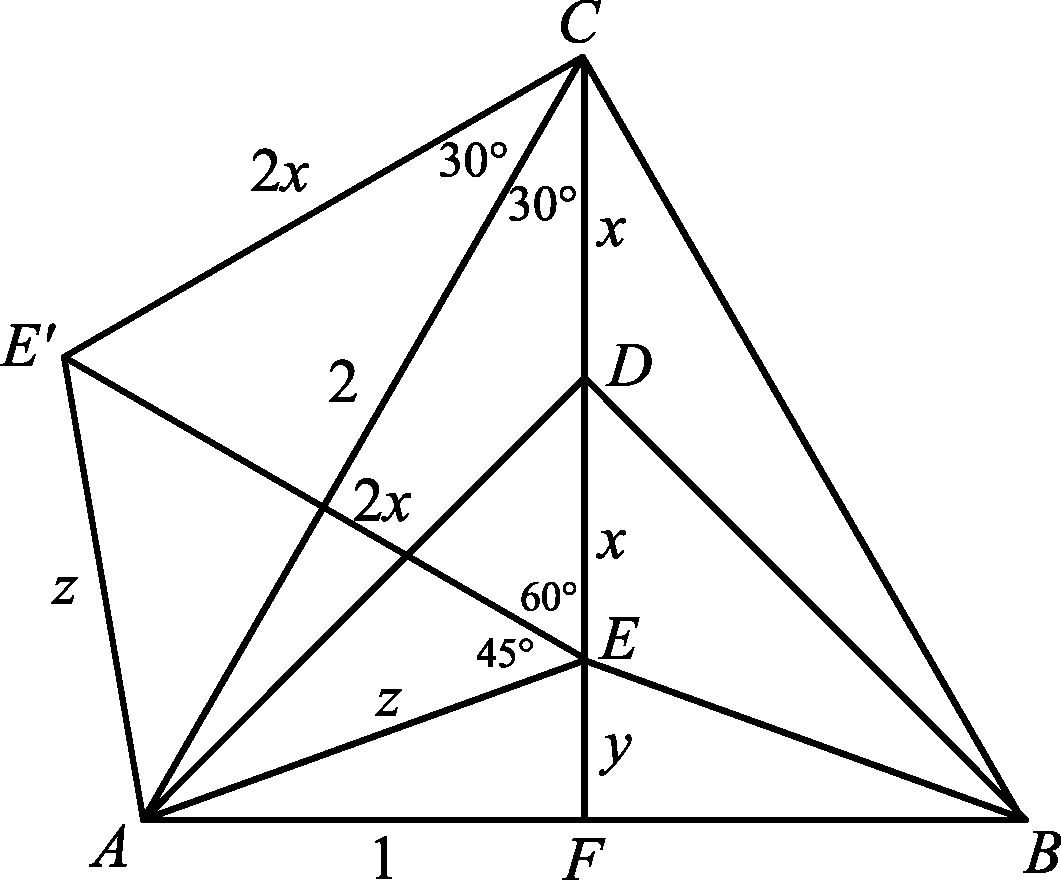
Az ![]() háromszögben a Pitagorasz-tétel miatt
háromszögben a Pitagorasz-tétel miatt
az ![]() háromszög egyenlő szárú, így
háromszög egyenlő szárú, így
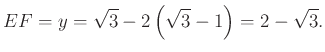
az ![]() háromszögben a Pitagorasz-tétel miatt
háromszögben a Pitagorasz-tétel miatt
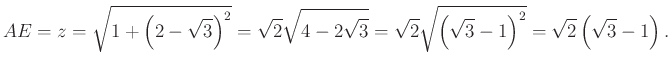
Legyen az ![]() pont tükörképe az
pont tükörképe az ![]() oldalra nézve
oldalra nézve ![]() .
.
Az ![]() háromszög szabályos,
háromszög szabályos,
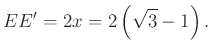
Az ![]() háromszögben
háromszögben
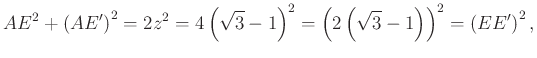
ezért ez a háromszög a Pitagorasz-tétel megfordítása miatt derékszögű. Mivel egyenlő szárú is, ezért
Mivel az
ezért az
A kérdezett szög tehát:
6. megoldás
Legyen a háromszög oldala 2 egység. Használjuk az ábra jelöléseit.
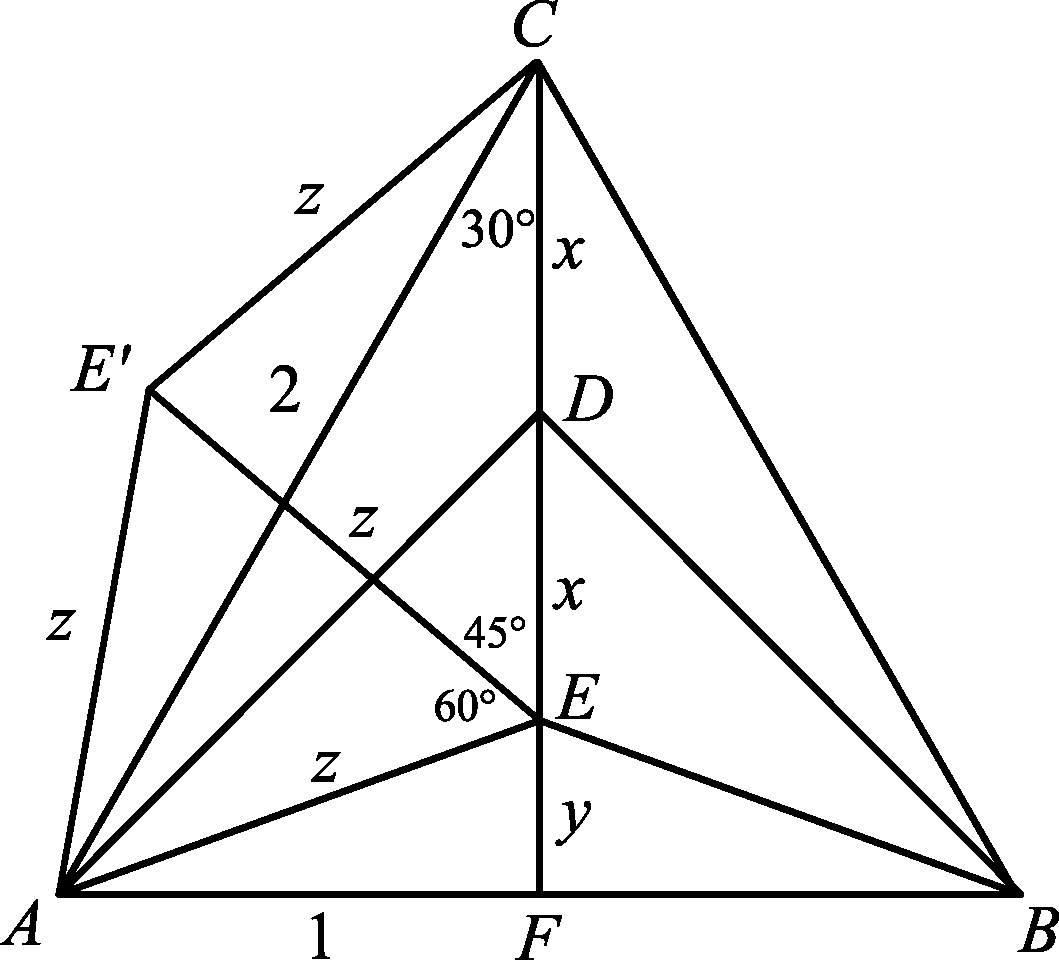
Az ![]() háromszögben a Pitagorasz-tétel miatt
háromszögben a Pitagorasz-tétel miatt
az ![]() háromszög egyenlő szárú, így
háromszög egyenlő szárú, így
ezért
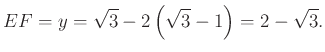
Az ![]() háromszögben a Pitagorasz-tétel miatt
háromszögben a Pitagorasz-tétel miatt
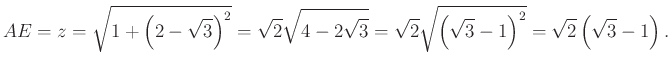
Forgassuk el az ![]() háromszöget 60 fokkal az
háromszöget 60 fokkal az ![]() pont körül.
pont körül.
Legyen az ![]() pont elforgatottja
pont elforgatottja ![]() . Az
. Az ![]() háromszög szabályos,
háromszög szabályos,
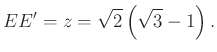
A ![]() háromszögben
háromszögben
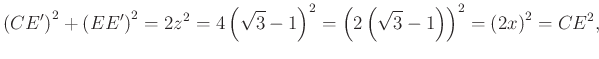
ezért ez a háromszög a Pitagorasz-tétel megfordítása miatt derékszögű. Mivel ez a háromszög egyenlő szárú is, ezért
Mivel az ![]() , ezért az
, ezért az ![]() . A kérdezett szög tehát:
. A kérdezett szög tehát:
7. megoldás
Tekintsük az ![]() szabályos sokszöget, amelynek középpontja
szabályos sokszöget, amelynek középpontja ![]() pont.
pont.
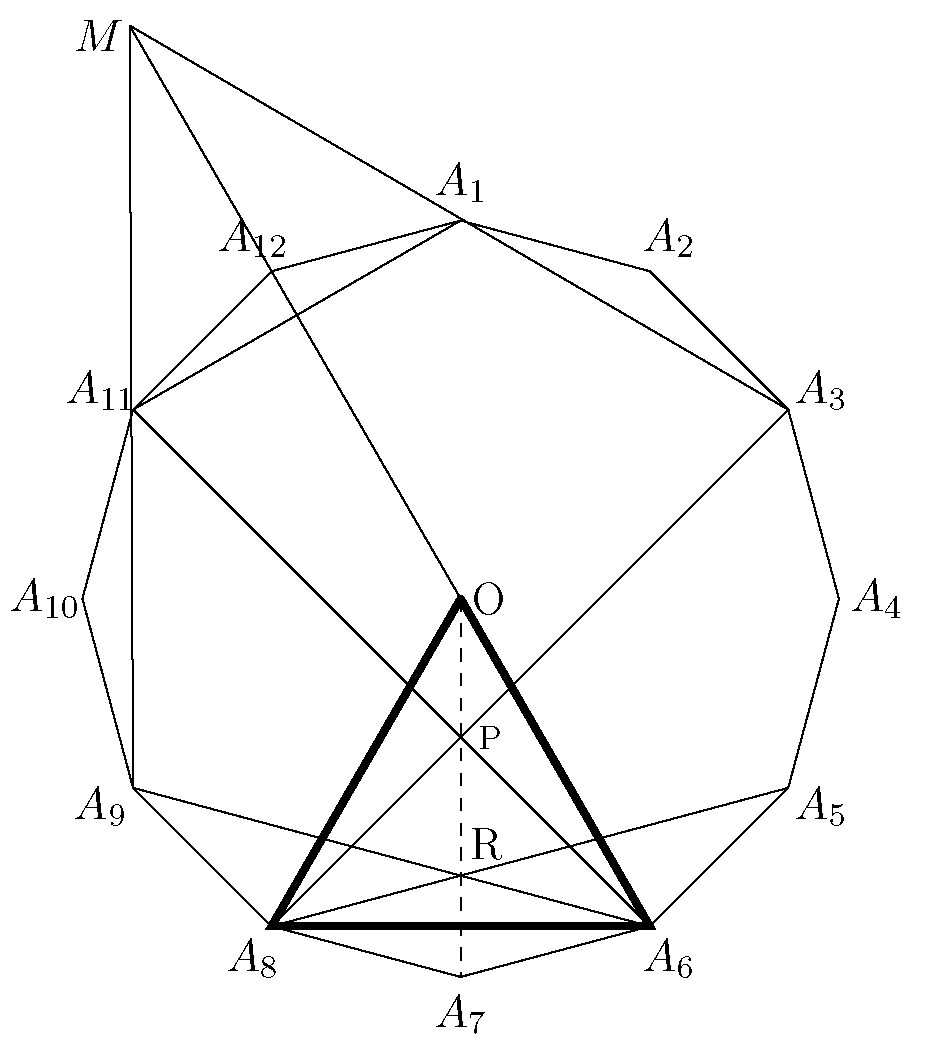
Az ![]() szakasz
szakasz ![]() körüli 90 fokos elforgatottja az
körüli 90 fokos elforgatottja az ![]() szakasz, így ez a két szakasz merőleges. Mivel az említett két szakasz egymás tükörképe az
szakasz, így ez a két szakasz merőleges. Mivel az említett két szakasz egymás tükörképe az ![]() egyenesre, így
egyenesre, így ![]() metszéspontjuk illeszkedik a tükörtengelyre, tehát
metszéspontjuk illeszkedik a tükörtengelyre, tehát
Hasonlóan az ![]() szakasz
szakasz ![]() körüli 30 fokos elforgatottja az
körüli 30 fokos elforgatottja az ![]() szakasz, így ennek a két szakasznak a hajlásszöge
szakasz, így ennek a két szakasznak a hajlásszöge ![]() . Mivel az említett két szakasz egymás tükörképe az
. Mivel az említett két szakasz egymás tükörképe az ![]() egyenesre, így
egyenesre, így ![]() metszéspontjuk illeszkedik a tükörtengelyre, tehát
metszéspontjuk illeszkedik a tükörtengelyre, tehát ![]() , azaz
, azaz
Mivel ![]() egy szabályos hatszög, ezért minden oldala egyenlő a köré írt kör sugarával (
egy szabályos hatszög, ezért minden oldala egyenlő a köré írt kör sugarával (![]() ), továbbá belső szögei 120 fokosak, tehát az
), továbbá belső szögei 120 fokosak, tehát az ![]() háromszög szabályos, ezért
háromszög szabályos, ezért
Az ![]() négyszög rombusz, mivel minden oldala
négyszög rombusz, mivel minden oldala ![]() hosszúságú, ezért szemközti oldalai,
hosszúságú, ezért szemközti oldalai, ![]() és
és ![]() párhuzamosak. Ez viszont azt jelenti, hogy egy
párhuzamosak. Ez viszont azt jelenti, hogy egy ![]() középpontú kicsinyítéssel az
középpontú kicsinyítéssel az ![]() szakasz képe lehet az
szakasz képe lehet az ![]() szakasz, akkor a vele egyenlő hosszú
szakasz, akkor a vele egyenlő hosszú ![]() szakasz képe ugyanezen kicsinyítés során az
szakasz képe ugyanezen kicsinyítés során az ![]() szakasz, így
szakasz, így
Mivel ![]() , így megjelent az ábrán a feladatban szereplő valamennyi pont és vonal: legyen
, így megjelent az ábrán a feladatban szereplő valamennyi pont és vonal: legyen ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
A kérdezett szög tehát:
Megjegyzés: Természetesen a megoldás során tett állítások kerületi és középponti szögek tételére való hivatkozással is indokolhatók.
Zárszó
Kedves Olvasó! Ha egy másik „szép” megoldást talál, kérem küldje el nekem a Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát. e-mail címre. Ezeket az újabb megoldásokat összegyűjtve időnként (terveim szerint) szintén megmutatnám.
Szoldatics József
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium









