A 2017. évi székesfehérvári Rátz László matematikatanári vándorgyűlésen elhangzott előadás szerkesztett változata. Az Érintő 2017. szeptemberi számában megjelent első rész folytatása.
Mottó: „A legtöbb amit a tanár a diákjaiért tehet az, hogy észrevétlenül rávezeti egy-egy jó ötletre.” (Pólya György) A kérdéseket először mi tesszük fel, majd fokozatosan érjük el, hogy ezeket már a tanulók maguk fogalmazzák meg. Ha ezt következetesen csináljuk, akkor eljuthatunk ahhoz az örömteli helyzethez, hogy a tanítványaink olyan érdekes kérdéseket is fel tudnak tenni, ami nekünk nem is jutott eszünkbe.
A cikk első részében példákat hoztam néhány javasolt kérdésre, amit célszerű feltenni:
I. Lehet-e a feladatnak több, más eredménye is?
II. Lehet-e más módszerrel eredményre jutni? Melyik módszer a legalkalmasabb, melyik ragadja meg leginkább a feladat lényegét? Milyen más feladatokban vezethet eredményre a megoldásban alkalmazott módszer? Szükség volt-e a megoldáshoz minden feltételre? Lehet-e a problémát általánosítani?
A második részben további kérdésekre mutatok feladatokat:
III. Megfordítható-e az állítás?
IV. Hogyan változhat a feladat eredménye, vagy megoldási módszere, ha a feltételeket kissé módosítjuk?
V. Milyen alkalmazásai lehetnek a megoldott problémának?
III. Megfordítható-e az állítás?
Általános- és középiskolában sok olyan tétellel találkoznak a tanulók, amelyeknek a megfordítása is igaz, de az nem szerepel a tananyagban. Az alkalmazásnál viszont gyakori, hogy a bizonyított tétel helyett annak megfordítását használják fel. Feladatoknál pedig még gyakoribb, hogy a feladat szövege csak az egyik irányú állítás igazolására szólít fel.
Akár tételként, akár feladatként találkoznak tanítványaink Ha ..., akkor ... típusú állításokkal, célszerű megvizsgálni, hogy igaz-e az állítás megfordítása?
A következőkben néhány olyan, négyszögekre vonatkozó állítást vizsgálunk, amelyeket jobb osztályokban tételként szoktunk bizonyítani, illetve más csoportokban is előkerülhetnek feladatként, de megfordításuk általában nem szerepel a tananyagban. A tételek bizonyítását ismertnek tekintjük, itt csak a megfordításokkal foglakozunk.
III/1. feladat. Tudjuk, hogy a paralelogramma oldalainak négyzetösszege egyenlő az átlók négyzetösszegével. Igaz-e, hogy ha egy konvex négyszög oldalainak négyzetösszege egyenlő az átlók négyzetösszegével, akkor a négyszög paralelogramma?
Megoldás. A megfordítás is igaz. Ennek megmutatásához egy általánosabb tételt igazolunk:
Ha az ![]() konvex négyszög
konvex négyszög ![]() és
és ![]() átlóinak felezőpontja
átlóinak felezőpontja ![]() és
és ![]() , akkor
, akkor
1. bizonyítás. 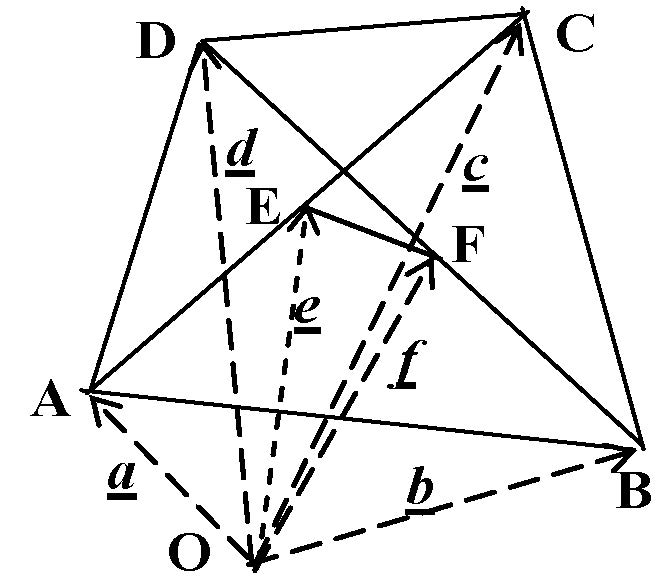 A sík tetszőleges
A sík tetszőleges ![]() pontjából az
pontjából az ![]() ,
, ![]() ,
, ![]() és
és ![]() pontokba mutató vektorok legyenek
pontokba mutató vektorok legyenek ![]() ,
, ![]() ,
, ![]() és
és ![]() .
.
Ekkor ![]() -ból az
-ból az ![]() és
és ![]() pontba mutató vektorok
pontba mutató vektorok 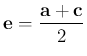 és
és 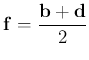 .
.
Így a fenti állítás
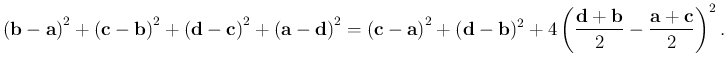
A műveleteket elvégezve a két oldal egyenlő.
2. bizonyítás. Helyezzük el a négyszöget koordináta-rendszerbe, és legyen ![]() ,
, ![]() ,
, ![]() és
és ![]() . Ekkor
. Ekkor 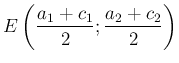 és
és 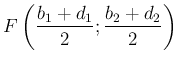 , továbbá
, továbbá ![]() , ...
, ...
A megfelelő koordinátákat az igazolandó állításba írva láthatjuk, hogy a két oldal egyenlő.
Az igazolt tételből következik, hogy ha a négyszög oldalainak négyzetösszege egyenlő az átlók négyzetösszegével, akkor ![]() , azaz a négyszög paralelogramma. Sőt az is, hogy ha a négyszög nem paralelogramma, akkor a négyszög oldalainak négyzetösszege nagyobb az átlók négyzetösszegénél.
, azaz a négyszög paralelogramma. Sőt az is, hogy ha a négyszög nem paralelogramma, akkor a négyszög oldalainak négyzetösszege nagyobb az átlók négyzetösszegénél.
III/2. feladat. Tudjuk, hogy húrnégyszögben a két átlón az átlódarabok szorzata egyenlő. Igaz-e, hogy ha egy konvex négyszögben a két átlón az átlódarabok szorzata egyenlő, akkor a négyszög húrnégyszög?
Megoldás. 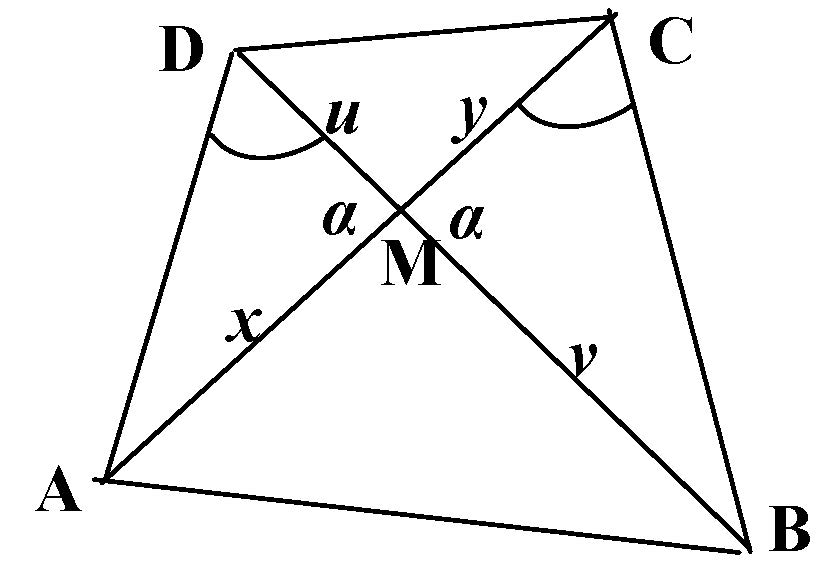 A megfordítás is igaz.
A megfordítás is igaz.
Ha ![]() , akkor
, akkor 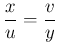 .
.
Az ![]() és
és ![]() háromszögek hasonlók, mert két oldaluk aránya egyenlő, és az oldalak által közbezárt szög mindkét háromszögben
háromszögek hasonlók, mert két oldaluk aránya egyenlő, és az oldalak által közbezárt szög mindkét háromszögben ![]() .
.
Ezért a megfelelő szögek is egyenlők: ![]() .
.
Ha egy oldal a másik két csúcsból azonos szög alatt látszik, akkor a négyszög húrnégyszög.
III/3. feladat. Tudjuk, hogy húrnégyszögben az átlók szorzata egyenlő a szemközti oldalak szorzatának összegével. Igaz-e, hogy ha egy konvex négyszögben az átlók szorzata egyenlő a szemközti oldalak szorzatának összegével, akkor a négyszög húrnégyszög?
Megoldás. 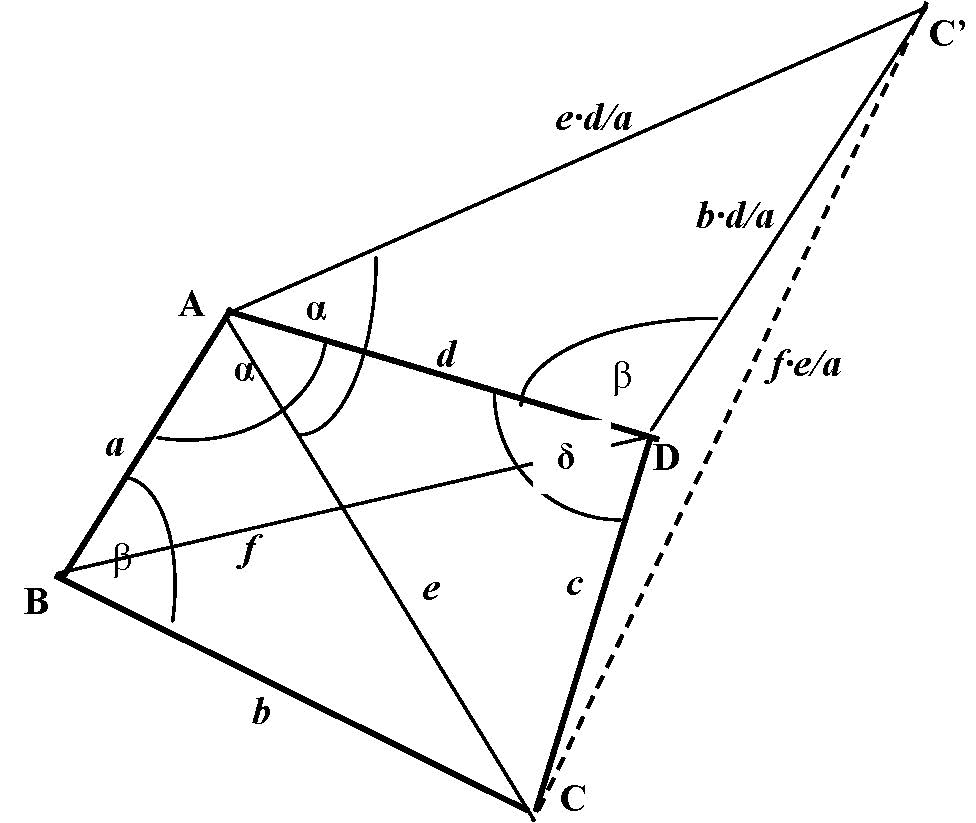 A megfordítás is igaz. Ennek megmutatásához is egy általánosabb tételt igazolunk:
A megfordítás is igaz. Ennek megmutatásához is egy általánosabb tételt igazolunk:
Minden konvex négyszögben az átlók szorzata nem nagyobb a szemközti oldalak szorzatának összegénél. Egyenlőség akkor és csak akkor állhat fenn, ha a négyszög húrnégyszög.
Bizonyítás forgatva nyújtás segítségével. Alkalmazzuk az ![]() háromszögre az
háromszögre az 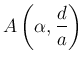 forgatva nyújtást. Ennél
forgatva nyújtást. Ennél ![]() képe
képe ![]() ,
, ![]() képe
képe ![]() .
.
A ![]() -szoros nyújtás miatt
-szoros nyújtás miatt 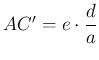 és
és 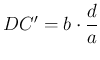 . A forgatás miatt
. A forgatás miatt ![]() és
és ![]() ,
,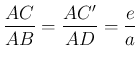 . Ezért
. Ezért ![]() . Így a harmadik oldalak aránya is
. Így a harmadik oldalak aránya is ![]() , azaz
, azaz 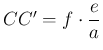 . A
. A ![]() (esetleg elfajuló) háromszögben:
(esetleg elfajuló) háromszögben:
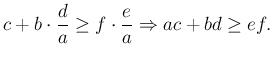
Egyenlőség akkor és csak akkor állhat, ha ![]() , azaz ha a négyszög húrnégyszög.
, azaz ha a négyszög húrnégyszög.
III/4. feladat. Tudjuk, hogy ha egy konvex négyszög átlói merőlegesek, akkor a szemközti oldalak négyzetösszege egyenlő. Igaz-e, hogy ha egy konvex négyszögben a szemközti oldalak négyzetösszege egyenlő, akkor a négyszög átlói merőlegesek?
Megoldás. 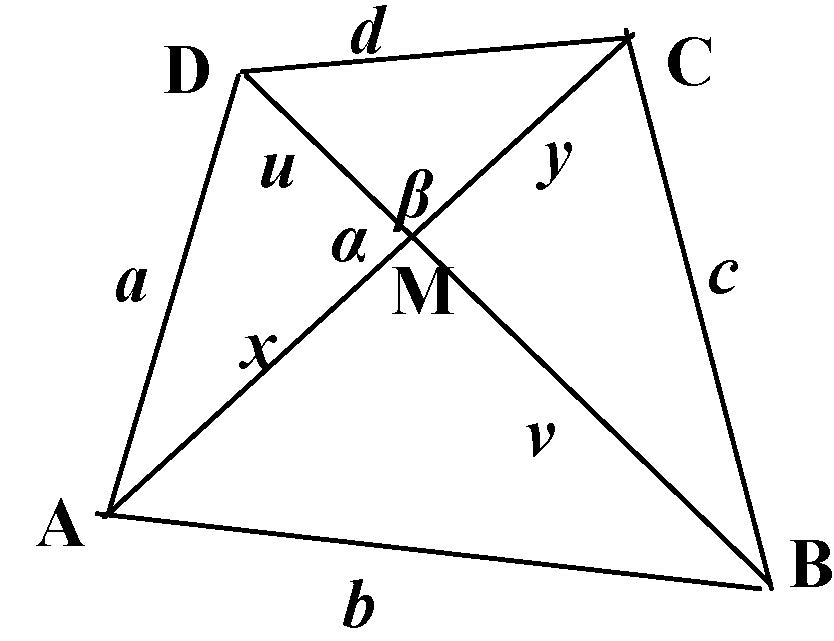 A megfordítás is igaz. Ezt indirekt módszerrel mutatjuk meg.
A megfordítás is igaz. Ezt indirekt módszerrel mutatjuk meg.
Tegyük fel, hogy az állítás nem igaz: ![]() , de az átlók nem merőlegesek. Feltehetjük, hogy pl.
, de az átlók nem merőlegesek. Feltehetjük, hogy pl. ![]() ,
, ![]() .
.
Ekkor ![]() ,
, ![]() és
és ![]() ,
, ![]() .
.
Ezekből ![]() . Ez ellentmond annak, hogy
. Ez ellentmond annak, hogy ![]() .
.
Megjegyzés. Vektorokkal vagy koordináta-rendszerben való elhelyezéssel megmutatható, hogy a tétel is és a megfordítása is (nem hurkolt) konkáv négyszögekben is igaz, sőt nem síkbeli négyszögekre is.
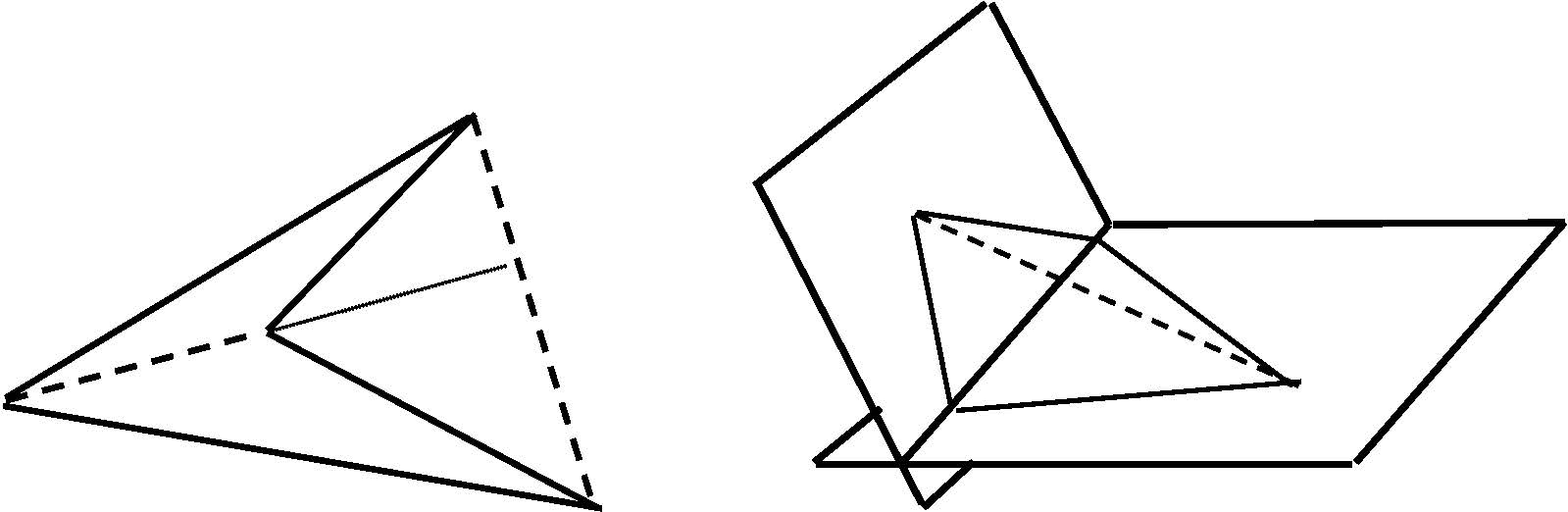
III/5. feladat. Tudjuk, hogy az ![]() téglalap síkjának tetszőleges
téglalap síkjának tetszőleges ![]() pontjára
pontjára ![]() .
.
Igaz-e, hogy ha az ![]() négyszög síkjának tetszőleges
négyszög síkjának tetszőleges ![]() pontjára
pontjára ![]() , akkor a négyszög téglalap?
, akkor a négyszög téglalap?
(Lásd KöMaL 2008. szept. B.4106. feladat.)
Megoldás. A megfordítás is igaz.
Vegyük fel a ![]() pontot először a négyszög
pontot először a négyszög ![]() csúcsában, ekkor
csúcsában, ekkor ![]() .
.
Ha ![]() , akkor
, akkor ![]() , ezekből
, ezekből
Ugyanígy, ha ![]() -t a másik átló végpontjaiban vesszük fel, akkor
-t a másik átló végpontjaiban vesszük fel, akkor
Az (1) és a (2) egyenlőséget összeadva, illetve kivonva, azt kapjuk, hogy ![]() , illetve
, illetve ![]() , tehát a négyszög paralelogramma.
, tehát a négyszög paralelogramma.
Vegyük fel ezután a ![]() pontot a paralelogramma átlóinak metszéspontjában. Mivel az átlók felezik egymást, azt kapjuk, hogy pl.
pontot a paralelogramma átlóinak metszéspontjában. Mivel az átlók felezik egymást, azt kapjuk, hogy pl. ![]() , az átlók egyenlők, a négyszög valóban téglalap.
, az átlók egyenlők, a négyszög valóban téglalap.
Megjegyzés. Az eredeti állítás a tér tetszőleges ![]() pontja esetén igaz, és így természetesen a megfordítás is igaz akkor is, ha
pontja esetén igaz, és így természetesen a megfordítás is igaz akkor is, ha ![]() a tér tetszőleges pontja.
a tér tetszőleges pontja.
A következőkben a fenti öt tétel alkalmazására mutatunk feladatokat. Olyanokat is, amelyeknél a fenti tételek segíthettek emelt szintű érettségin és versenyeken is szép megoldások megtalálásában.
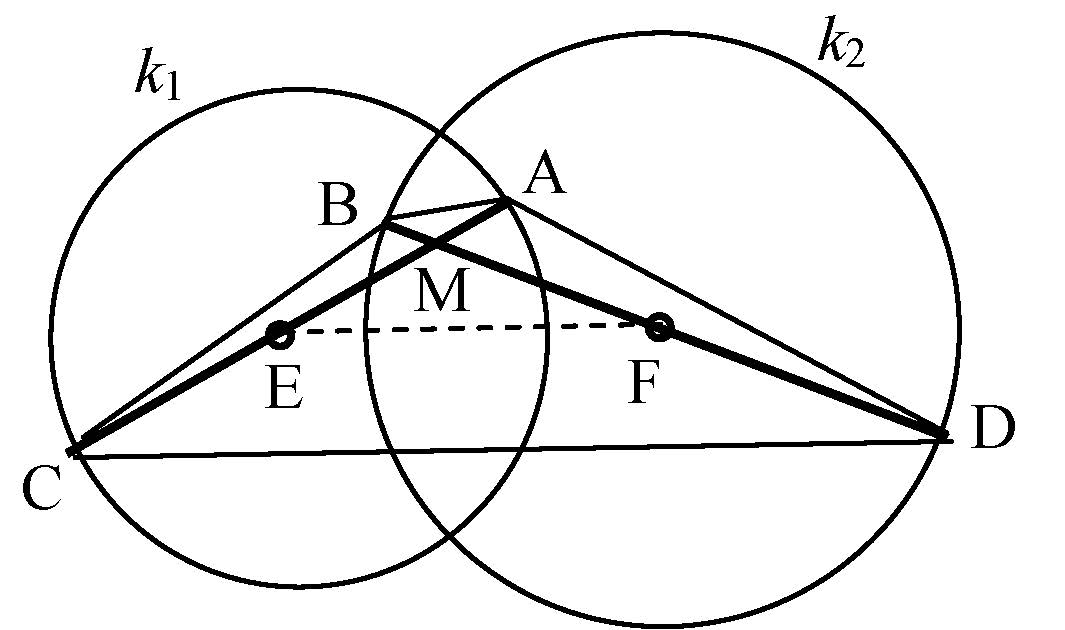 III/6. feladat. Az
III/6. feladat. Az ![]() egység sugarú
egység sugarú ![]() és a
és a ![]() egység sugarú
egység sugarú ![]() körök középpontjainak távolsága
körök középpontjainak távolsága ![]() egység. A
egység. A ![]() kör
kör ![]() átmérője és a
átmérője és a ![]() kör
kör ![]() átmérője
átmérője ![]() -ben metszi egymást. Mekkora az
-ben metszi egymást. Mekkora az ![]() négyszög oldalainak négyzetösszege?
négyszög oldalainak négyzetösszege?
Megoldás. A III/1. feladat megoldásában bizonyított tétel szerint
III/7. feladat. Az ![]() konvex négyszög oldalegyeneseinek egyenlete rendre:
konvex négyszög oldalegyeneseinek egyenlete rendre: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
a) Igazolja, hogy a négyszög átlói az ![]() és az
és az ![]() tengelyre illeszkednek, továbbá hogy ennek a négyszögnek nincsen derékszöge!
tengelyre illeszkednek, továbbá hogy ennek a négyszögnek nincsen derékszöge!
b) Bizonyítsa be, hogy ez a négyszög húrnégyszög! (A 2010. évi májusi emelt szintű érettségi 7. feladata.)
Megoldás.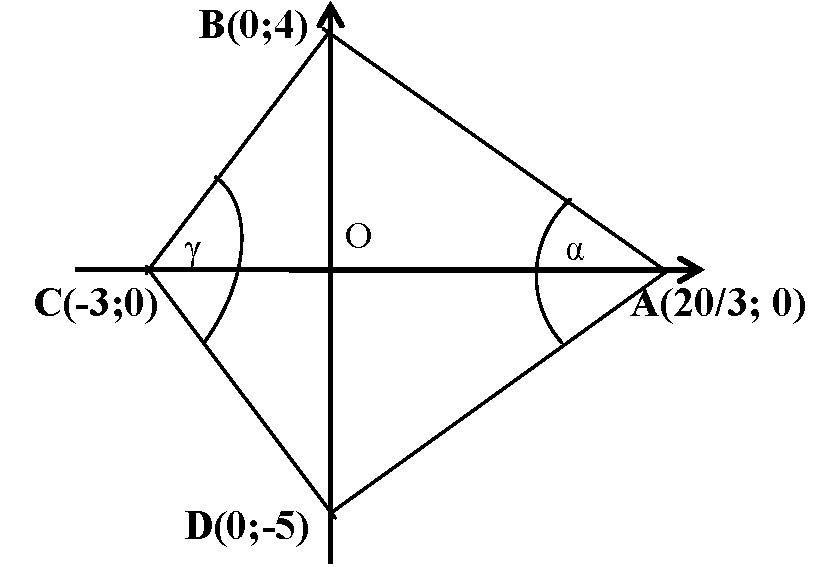 a) A megfelelő egyenletrendszerek megoldásával kiszámolhatjuk a csúcsok koordinátáit:
a) A megfelelő egyenletrendszerek megoldásával kiszámolhatjuk a csúcsok koordinátáit:
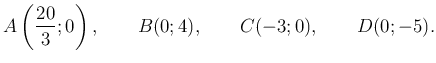
Tehát a csúcsok valóban a tengelyekre illeszkednek.
Az oldalegyenesek irányvektorai:
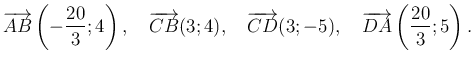
Ezekből
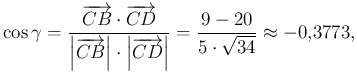
ezért ![]() . Hasonló módszerrel
. Hasonló módszerrel ![]() .
.
A ![]() és
és ![]() csúcsban találkozó oldalak irányvektorainak skalárszorzata sem 0, ezért nincs derékszög a négyszögben.
csúcsban találkozó oldalak irányvektorainak skalárszorzata sem 0, ezért nincs derékszög a négyszögben.
b) Aki a fentiekből ![]() kiszámolásával igazolta, hogy a négyszög húrnégyszög, az nem kapott pontot, mert a közelítő értékek nem bizonyítják az állítást.
kiszámolásával igazolta, hogy a négyszög húrnégyszög, az nem kapott pontot, mert a közelítő értékek nem bizonyítják az állítást.
Ez a gondolatmenet akkor elfogadható, ha ![]() és
és ![]() pontos értékéről állapítjuk meg, hogy egymásnak
pontos értékéről állapítjuk meg, hogy egymásnak ![]() -szeresei.
-szeresei.
Hasonlóan jó megoldás az is, ha pl. a ![]() és
és ![]() hegyesszögek tangenseiről mutatjuk meg, hogy egyenlők.
hegyesszögek tangenseiről mutatjuk meg, hogy egyenlők.
Sokkal egyszerűbben jutunk eredményre, ha a III/2. feladat állításának felhasználásával megmutatjuk, hogy 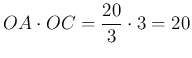 , és
, és ![]() , azaz
, azaz ![]() , ezért a négyszög húrnégyszög.
, ezért a négyszög húrnégyszög.
III/8. feladat Az ![]() háromszög szabályos.
háromszög szabályos.
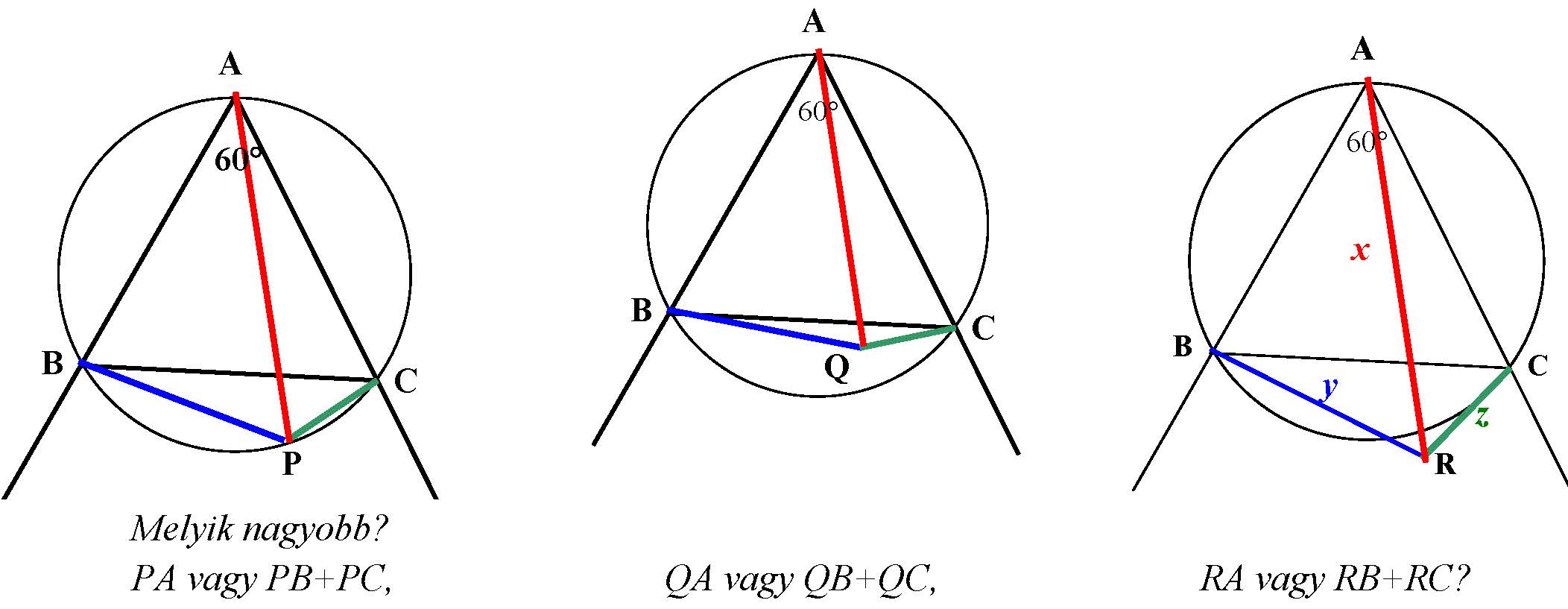
Megoldás. A III/3. feladat megoldásában bizonyított tétel szerint húrnégyszögben a szemközti oldalak szorzatának összege egyenlő az átlók szorzatával, ha a négyszög nem húrnégyszög, akkor szemközti oldalak szorzatának összege nagyobb az átlók szorzatánál.
Ezért ha a szabályos háromszög oldala ![]() , akkor
, akkor ![]() , azaz
, azaz ![]() .
.
A másik két ábrán viszont a ![]() és
és ![]() négyszögek nem húrnégyszögek, ezért
négyszögek nem húrnégyszögek, ezért ![]() , azaz
, azaz ![]() , illetve
, illetve ![]() , azaz
, azaz ![]() .
.
Megjegyzés. A feladatban a tanulók igen nagy százalékban a ![]() ,
, ![]() , illetve
, illetve ![]() megoldást adták meg.
megoldást adták meg.
III/9. feladat. Ha egy csuklós négyszög átlói valamely helyzetben merőlegesek, akkor minden helyzetben merőlegesek.
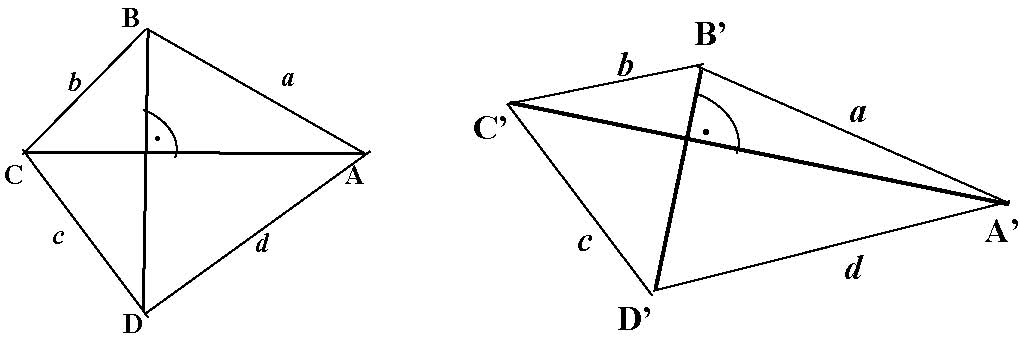
Megoldás. Ha az ![]() négyszögben az átlók merőlegesek, akkor
négyszögben az átlók merőlegesek, akkor ![]() .
.
De ha ![]() , akkor az
, akkor az ![]() négyszögben az átlók merőlegesek, azaz minden helyzetben merőlegesek.
négyszögben az átlók merőlegesek, azaz minden helyzetben merőlegesek.
III/10. feladat. Adott a síkban egy ![]() kör és a körön belül egy
kör és a körön belül egy ![]() pont. Mi lesz az összes olyan
pont. Mi lesz az összes olyan ![]() téglalap
téglalap ![]() csúcsának mértani helye, amelyeknek
csúcsának mértani helye, amelyeknek ![]() és
és ![]() csúcsa illeszkedik a
csúcsa illeszkedik a ![]() körre?
körre?
(Lásd KöMaL 2002. nov. B.3588. feladat.)
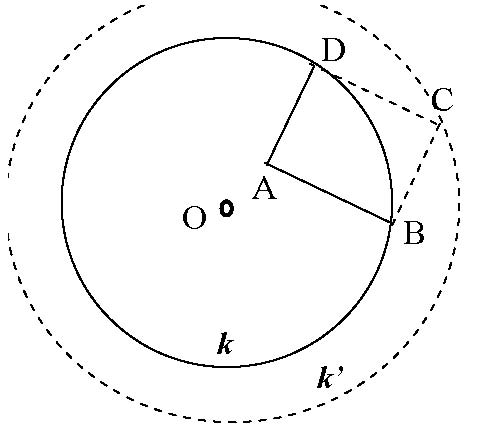 Megoldás. Alkalmazzuk a III/5. feladatot úgy, hogy a
Megoldás. Alkalmazzuk a III/5. feladatot úgy, hogy a ![]() pont a kör
pont a kör ![]() középpontja legyen:
középpontja legyen: ![]() .
.
Mivel ![]() minden helyzetben a kör sugarával egyenlő, és
minden helyzetben a kör sugarával egyenlő, és ![]() is állandó, ezért
is állandó, ezért ![]() is állandó. Tehát a
is állandó. Tehát a ![]() pont mértani helye egy
pont mértani helye egy ![]() középpontú
középpontú ![]() sugarú
sugarú ![]() kör.
kör.
Mivel ![]() , ezért
, ezért ![]() bármely helyzetében
bármely helyzetében ![]() .
.
A ![]() kör minden
kör minden ![]() pontja hozzá tartozik a mértani helyhez, az
pontja hozzá tartozik a mértani helyhez, az ![]() szakasz Thalész-köre kimetszi a
szakasz Thalész-köre kimetszi a ![]() körön a megfelelő
körön a megfelelő ![]() és
és ![]() pontokat.
pontokat.
Megjegyzés. Ha nem kötjük, ki, hogy ![]() a
a ![]() kör belső pontja, akkor csak abban az esetben van megoldás, ha
kör belső pontja, akkor csak abban az esetben van megoldás, ha ![]() . Ha
. Ha ![]() , akkor a keresett mértani hely az
, akkor a keresett mértani hely az ![]() pont.
pont.
Néhány további gyakorló feladat
III/11. feladat. a) Tudjuk, hogy egy rombusznak két szimmetriatengelye van, a két átlója. Igaz-e, hogy ha egy négyszög alakú ruhadarabról hajtogatással akarjuk eldönteni, hogy rombusz alakú-e, akkor ehhez legalább két hajtást kell végezni?
b) Tudjuk, hogy egy téglalapnak két szimmetriatengelye van. Igaz-e, hogy ha egy négyszög alakú ruhadarabról hajtogatással akarjuk eldönteni, hogy téglalap alakú-e, akkor ehhez legalább két hajtást kell végezni?
c) Tudjuk, hogy egy négyzetnek négy szimmetriatengelye van. Igaz-e, hogy ha egy négyszög alakú ruhadarabról hajtogatással akarjuk eldönteni, hogy négyzet alakú-e, akkor ehhez legalább négy hajtást kell végezni?
III/12. feladat. Az ![]() konvex négyszög átlóinak metszéspontja
konvex négyszög átlóinak metszéspontja ![]() . Tudjuk, hogy ha
. Tudjuk, hogy ha ![]() , akkor a
, akkor a ![]() és
és ![]() háromszögek területe egyenlő. Igaz-e, hogy ha a
háromszögek területe egyenlő. Igaz-e, hogy ha a ![]() és
és ![]() háromszögek területe egyenlő, akkor
háromszögek területe egyenlő, akkor ![]() ?
?
III/13. feladat. Az ![]() konvex négyszög
konvex négyszög ![]() oldalának felezőpontja
oldalának felezőpontja ![]() . Tudjuk, hogy ha
. Tudjuk, hogy ha ![]() akkor az
akkor az ![]() háromszög területe fele a négyszög területének. Igaz-e, hogy ha az
háromszög területe fele a négyszög területének. Igaz-e, hogy ha az ![]() háromszög területe fele a négyszög területének, akkor
háromszög területe fele a négyszög területének, akkor ![]() ?
?
IV. Hogyan változik a feladat eredménye, megoldási módszere, ha kissé változtatunk a feltételeken?
Egy feladat teljesebb megértését szolgálja, ha megvizsgáljuk, hogyan változik az eredmény, esetleg a megoldási módszer, ha a feltételeket kissé megváltoztatjuk. Célszerű tanítványainkat rászoktatni arra, hogy elemezzék, módosítsák a feltételeket. Nemcsak azért, mert ezáltal világosabbá válik, hogy melyik feltételnek milyen szerepe van a feladatban, hanem azért is, mert ez az egyszerű elvárás jól fejleszti a kreativitást, és meglepő új problémákhoz vezethet.
A kétszemélyes matematikai játékok témaköréből mutatunk néhány példát arra, hogy a feltételek kisebb módosításával változatos feladatcsokrokat hozhatunk létre. Az első két feladat megoldását az olvasóra bízzuk, ill. megtalálhatók [6]-ban. Javasoljuk további módosítások elemzését. (Mindegyik feladatban a lehetséges lépéseket fogalmazzuk meg, de lépni kötelező, passzolni nem lehet.)
IV/1. feladat. a) Egy asztalon ![]() kavics van. Ketten felváltva vesznek el kavicsokat. Egy lépésben
kavics van. Ketten felváltva vesznek el kavicsokat. Egy lépésben ![]() ,
, ![]() vagy
vagy ![]() kavicsot. Az a játékos nyer, aki az utolsó kavicsot elveszi. Ki tud nyerni, Kezdő vagy Második?
kavicsot. Az a játékos nyer, aki az utolsó kavicsot elveszi. Ki tud nyerni, Kezdő vagy Második?
Legyen az asztalon levő kavicsok száma ![]() , az egy lépésben elvehető kavicsok száma
, az egy lépésben elvehető kavicsok száma ![]() . Ki tud nyerni, ha
. Ki tud nyerni, ha
b) ![]() ,
, ![]() ,
,
c) ![]() ,
, ![]() ,
,
d) Milyen ![]() számpároknál tud Kezdő nyerni?
számpároknál tud Kezdő nyerni?
e) Hogyan módosul a feladat a fenti esetekben, ha az veszít, aki az utolsó kavicsot elveszi?
f*) ![]() és
és ![]() esetén ki tud nyerni, ha az nyer, akinél a végén páros számú kavics lesz?
esetén ki tud nyerni, ha az nyer, akinél a végén páros számú kavics lesz?
g) ![]() esetén ki tud nyerni, ha az elvehető kavicsok száma
esetén ki tud nyerni, ha az elvehető kavicsok száma ![]() vagy
vagy ![]() ? (Így nemcsak az nyer, aki az utolsó kavicsot elveszi, hanem az is, aki 1 kavicsot hagy az asztalon.)
? (Így nemcsak az nyer, aki az utolsó kavicsot elveszi, hanem az is, aki 1 kavicsot hagy az asztalon.)
h*) Adott ![]() esetén az elvehető kavicsok száma
esetén az elvehető kavicsok száma ![]() vagy
vagy ![]() . Milyen
. Milyen ![]() számpároknál tud Kezdő nyerni? (Az nyer, aki a végén az asztalon
számpároknál tud Kezdő nyerni? (Az nyer, aki a végén az asztalon ![]() kavicsot hagy.)
kavicsot hagy.)
i) ![]() ,
, ![]() esetén ki nyer, ha nem szabad annyi kavicsot elvenni, amennyit az előző lépésben a partner elvett? (Nemcsak az nyer, aki az utolsó kavicsot elveszi, hanem az is, aki a végén az asztalon levő két kavicsból
esetén ki nyer, ha nem szabad annyi kavicsot elvenni, amennyit az előző lépésben a partner elvett? (Nemcsak az nyer, aki az utolsó kavicsot elveszi, hanem az is, aki a végén az asztalon levő két kavicsból ![]() -et elvesz, mert a partner nem tud már lépni.)
-et elvesz, mert a partner nem tud már lépni.)
j) Az asztalon van ![]() kavics. Az elvehető kavicsok száma az asztalon levő kavicsok legfeljebb fele. Milyen
kavics. Az elvehető kavicsok száma az asztalon levő kavicsok legfeljebb fele. Milyen ![]() estén tud nyerni Kezdő?
estén tud nyerni Kezdő?
k) Az asztalon van ![]() kavics. Az
kavics. Az ![]() -edik lépésben az elvehető kavicsok száma legfeljebb
-edik lépésben az elvehető kavicsok száma legfeljebb ![]() . Milyen
. Milyen ![]() estén tud nyerni Kezdő?
estén tud nyerni Kezdő?
IV/2. feladat. Az asztalon van két halom, az egyikben ![]() , a másikban
, a másikban ![]() kavics. A halmokból ketten felváltva vesznek el kavicsokat. Az nyer, aki az utolsó kavicsot elveszi. (Az veszít, aki a megengedett lépést már nem tudja elvégezni.) Milyen
kavics. A halmokból ketten felváltva vesznek el kavicsokat. Az nyer, aki az utolsó kavicsot elveszi. (Az veszít, aki a megengedett lépést már nem tudja elvégezni.) Milyen ![]() számpároknál tud Kezdő nyerni a következő feltételek esetén?
számpároknál tud Kezdő nyerni a következő feltételek esetén?
Egy lépésben szabad elvenni:
a) Az egyik halomból akármennyit. (Aki lép, az itt is, és a továbbiakban is mindig választhat, hogy melyik halomból veszi el a megengedett mennyiséget.)
b) Az egyik halomból akármennyit, vagy mindkét halomból ugyanannyit.
c) Az egyik halomból egyet.
d) Az egyik halomból egyet, vagy mindkét halomból egyet.
e) Az egyik halomból egyet vagy kettőt.
f) Az egyik halomból egyet vagy kettőt, vagy mindkét halomból egyet vagy kettőt.
g) Az egyik halomból egyet, a másik halomból kettőt.
Megjegyzés. A fenti feladatok átfogalmazhatók sakktáblás játékká. Egy sakktáblán valamelyik mezőre elhelyezünk egy bábut. A bábuval ketten felváltva lépnek, és az nyer, aki a bal alsó sarokba viszi a bábut. Távolodni nem szabad. A fenti a), c) és e) feladatokban a bábu bástya, a b) és f) feladatban vezér, a d) feladatban király, a g) feladatban huszár. A sakktáblán könnyebben megtalálhatjuk a nyerő és vesztő mezőket.
IV/3. feladat. Van egy ![]() kavicsból álló halmazunk. Egy lépés abból áll, hogy a halmazt két részre bontják. Ketten felváltva lépnek. Az veszít, aki a megengedett lépést már nem tudja elvégezni. (Tehát az nyer, aki a csupa egy kavicsból álló halmaz-rendszert el tudja érni.)
kavicsból álló halmazunk. Egy lépés abból áll, hogy a halmazt két részre bontják. Ketten felváltva lépnek. Az veszít, aki a megengedett lépést már nem tudja elvégezni. (Tehát az nyer, aki a csupa egy kavicsból álló halmaz-rendszert el tudja érni.)
a) Ki tud nyerni ![]() esetén?
esetén?
b) Milyen ![]() -ek esetén van Másodiknak nyerő stratégiája?
-ek esetén van Másodiknak nyerő stratégiája?
c) Ki tud nyerni, ha három halomban vannak kavicsok: ![]() ,
, ![]() és
és ![]() db?
db?
d) Ki tud nyerni, ha három halomban vannak kavicsok: ![]() ,
, ![]() és
és ![]() db?
db?
e) Ki tud nyerni ![]() kavics esetén, ha az asztalon levő halmok egyikét sem lehet két egyenlő halomra bontani? (Most az nyer, aki el tudja érni, hogy az asztalon csupa egy- és kételemű halom legyen.)
kavics esetén, ha az asztalon levő halmok egyikét sem lehet két egyenlő halomra bontani? (Most az nyer, aki el tudja érni, hogy az asztalon csupa egy- és kételemű halom legyen.)
f**) Milyen ![]() -ek esetén van Másodiknak nyerő stratégiája egy halomban levő
-ek esetén van Másodiknak nyerő stratégiája egy halomban levő ![]() számú kavics esetén, ha az asztalon levő halmok egyikét sem lehet két egyenlő halomra bontani?
számú kavics esetén, ha az asztalon levő halmok egyikét sem lehet két egyenlő halomra bontani?
Megoldás. Az a), b), c) és d) feladatok esetén igen egyszerű a megoldás, ha észrevesszük, hogy minden bontásnál a halmok száma 1-gyel nő, ezért a halmok számának paritása minden lépésnél megváltozik. Például az a) feladatban Kezdő első lépése után 2 halom, minden további lépése után páros számú halom lesz, ezért a 10 db 1 elemű halmot ő tudja létrehozni, ő nyer.
Vizsgáljuk most az f) feladatot, speciális esetként megkapjuk az ![]() esetére a választ.
esetére a választ.
![]() és
és ![]() esetén Kezdő veszít, mert már az első lépést sem tudja megtenni.
esetén Kezdő veszít, mert már az első lépést sem tudja megtenni.
![]() esetén Kezdő tud nyerni, mert 1–2 bontást végez, és ezzel befejeződik a játék.
esetén Kezdő tud nyerni, mert 1–2 bontást végez, és ezzel befejeződik a játék.
![]() esetén Kezdő csak 1–3 bontást végezhet, amelyből Második 1–2–1 bontással nyer.
esetén Kezdő csak 1–3 bontást végezhet, amelyből Második 1–2–1 bontással nyer.
Ha valamely ![]() esetén Második tud nyerni, akkor
esetén Második tud nyerni, akkor ![]() és
és ![]() esetén Kezdőnek van nyerő stratégiája, hiszen 1–
esetén Kezdőnek van nyerő stratégiája, hiszen 1–![]() , ill. 2–
, ill. 2–![]() bontással olyan helyzetet hoz létre, amelyből a következő, tehát Második veszít. (*) Eszerint
bontással olyan helyzetet hoz létre, amelyből a következő, tehát Második veszít. (*) Eszerint ![]() és
és ![]() esetén Kezdő nyer.
esetén Kezdő nyer.
![]() esetén Kezdő háromféleképpen kezdhet. 1–6 és 2–5 bontással az előző pont szerint vesztő helyzetbe kerül. Kezdő 3–4 bontásánál Második 1–2–4-re bont. Ezután Kezdő csak 1–2–1–3-at tud bontani, amiből Második 1–2–1–1–2 bontással nyer.
esetén Kezdő háromféleképpen kezdhet. 1–6 és 2–5 bontással az előző pont szerint vesztő helyzetbe kerül. Kezdő 3–4 bontásánál Második 1–2–4-re bont. Ezután Kezdő csak 1–2–1–3-at tud bontani, amiből Második 1–2–1–1–2 bontással nyer.
![]() és
és ![]() esetén Kezdő (*) szerint nyerni tud.
esetén Kezdő (*) szerint nyerni tud.
![]() esetén Kezdő szintén háromféleképp kezdhet. 1–9 és 2–8 bontással az előző pont szerint vesztő helyzetbe kerül. Kezdő 4–6 bontásánál Második 4–2–4-re bont. Ezután amit Kezdő csinál az egyik 4-es halommal, Második azt utánozza a másikkal, ezért ő nem veszít. Mivel a játék véges sok lépésben befejeződik ezért Második nyer.
esetén Kezdő szintén háromféleképp kezdhet. 1–9 és 2–8 bontással az előző pont szerint vesztő helyzetbe kerül. Kezdő 4–6 bontásánál Második 4–2–4-re bont. Ezután amit Kezdő csinál az egyik 4-es halommal, Második azt utánozza a másikkal, ezért ő nem veszít. Mivel a játék véges sok lépésben befejeződik ezért Második nyer.
![]() és
és ![]() esetén Kezdő ismét (*) szerint nyerni tud.
esetén Kezdő ismét (*) szerint nyerni tud.
Itt már sejteni lehet egy szabályosságot: ![]() , 2 és minden
, 2 és minden ![]() alakú számra Második nyer, a többi számra Kezdő. Sajnos ez nem igaz. Már
alakú számra Második nyer, a többi számra Kezdő. Sajnos ez nem igaz. Már ![]() -ra sem működik. Itt a sejtéstől eltérően Kezdő tud nyerni.
-ra sem működik. Itt a sejtéstől eltérően Kezdő tud nyerni.
Hogyan tovább?
Ha nem kötjük ki, hogy különböző részekre kell bontani a halmazt, akkor a játék igen könnyű, illetve nem is igazán érdekes, mert aki az elején kedvező helyzetben van, bárhogy is játszanak a játékosok, mindig az nyer.
Az a látszólag kis nehezítés, hogy nem lehet két egyenlő részre bontani a halmokat, teljesen megváltoztatja a játékot. Olyannyira, hogy tetszőleges ![]() -re az általános megoldás nem is ismert.
-re az általános megoldás nem is ismert.
![]() , 2, 4, 7, 10, 20, 23, 26 esetén Második nyer, de a következő, Második számára kedvező
, 2, 4, 7, 10, 20, 23, 26 esetén Második nyer, de a következő, Második számára kedvező ![]() értékek már jóval nagyobbak: 50, 53, 270, 273, 276, ...
értékek már jóval nagyobbak: 50, 53, 270, 273, 276, ...
![]() -ig összesen 42 Második számára kedvező helyzet ismert.
-ig összesen 42 Második számára kedvező helyzet ismert.
A következő, nem nehéz számelméleti feladat továbbgondolása, kis módosítása olyan problémára vezet, amelynek tudomásom szerint nem ismert a megoldása.
IV/4. feladat. Van-e olyan kettő-hatvány, amelynek tízes számrendszerbeli alakjában mind a tíz számjegy ugyanannyiszor szerepel?
Megoldás. Nincs, mert ha minden számjegy ![]() -szor szerepelne, akkor a számjegyek összege
-szor szerepelne, akkor a számjegyek összege ![]() lenne, a szám osztható lenne 3-mal, de
lenne, a szám osztható lenne 3-mal, de ![]() nem osztható 3-mal.
nem osztható 3-mal.
Módosítás. Van-e olyan három-hatvány, amelynek tízes számrendszerbeli alakjában mind a tíz számjegy ugyanannyiszor szerepel?
Erre a kérdésre nem találtunk olyan indokot, ami kizárná a létezést, de mostanáig számítógépes programmal sem találtunk megfelelő számot.
Most egy számelméleti feladatot és annak egy olyan módosítását vizsgáljuk, amely egy igen hasznos alkalmazáshoz vezetett.
IV/5. feladat. Az ![]() szám összes pozitív osztójának összege
szám összes pozitív osztójának összege ![]() . Mi lehet az
. Mi lehet az ![]() szám?
szám?
Megoldás. Az ![]() szám prímtényezős felbontásának ismeretében meghatározhatjuk pozitív osztóinak összegét: Ha
szám prímtényezős felbontásának ismeretében meghatározhatjuk pozitív osztóinak összegét: Ha ![]() , akkor pozitív osztóinak összege:
, akkor pozitív osztóinak összege:
A képlet ötletet adhat arra is, hogy hogyan határozzuk meg ![]() ismeretében
ismeretében ![]() prímosztóit.
prímosztóit.
![]() , ezért 5394-nek
, ezért 5394-nek ![]() osztója van. Ezek:
osztója van. Ezek:
| 1, | 2, | 3, | 6, | 29, | 31, | 58, | 62, |
| 5394, | 2697, | 1798, | 899, | 186, | 174, | 93, | 87 |
Azt kell megkeresnünk, hogy ezek közül melyek állíthatók elő valamely ![]() prímre
prímre ![]() alakban.
alakban.
![]() értékei
értékei ![]() és
és ![]() növekedésével gyorsan nőnek. Készítsünk egy táblázatot, amelyben az összes 5394-nél nem nagyobb
növekedésével gyorsan nőnek. Készítsünk egy táblázatot, amelyben az összes 5394-nél nem nagyobb ![]() érték szerepel.
érték szerepel.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| 2 | 3 | 7 | 15 | 31 | 63 | 127 | 255 | 511 | 1023 | 2047 | 4095 |
| 3 | 4 | 13 | 40 | 121 | 364 | 1093 | 3280 | ||||
| 5 | 6 | 31 | 156 | 781 | 3906 | ||||||
| 7 | 8 | 57 | 400 | 2801 | |||||||
| 11 | 12 | 133 | 1464 | ||||||||
| 13 | 14 | 183 | 2380 | ||||||||
| 17 | 18 | 307 | 5220 | ||||||||
| 73 | 74 | 5403 | |||||||||
| 5393 | 5394 |
(A ![]() és
és ![]() oszlopban nem írtunk ki minden számot. A táblázatban valójában 753 lehetséges
oszlopban nem írtunk ki minden számot. A táblázatban valójában 753 lehetséges ![]() érték szerepel.)
érték szerepel.)
A ![]() oszlop 503 számot tartalmaz, ezért érdemesebb azt megnézni, hogy a fenti osztók közül melyik lesz
oszlop 503 számot tartalmaz, ezért érdemesebb azt megnézni, hogy a fenti osztók közül melyik lesz ![]() alakú, azaz melyiknek lesz a kisebb szomszédja prím.
alakú, azaz melyiknek lesz a kisebb szomszédja prím.
Ezek: ![]() , 5, 61, 173 és 5393.
, 5, 61, 173 és 5393.
![]() -hoz
-hoz ![]() jó megoldás. Valóban,
jó megoldás. Valóban, ![]() .
.
![]() -hoz
-hoz ![]() -re
-re ![]() is jó. Valóban,
is jó. Valóban, ![]() .
.
![]() -hoz
-hoz ![]() -re
-re ![]() is jó. Valóban,
is jó. Valóban, ![]() .
.
![]() -hez tartozó társosztó, a 87 nem állítható elő a táblázatból.
-hez tartozó társosztó, a 87 nem állítható elő a táblázatból.
![]() -höz tartozó társosztó, a 899 sem állítható elő a táblázatból.
-höz tartozó társosztó, a 899 sem állítható elő a táblázatból.
![]() -höz tartozó társosztó, a 2697 sem állítható elő a táblázatból.
-höz tartozó társosztó, a 2697 sem állítható elő a táblázatból.
A ![]() oszlopokban szereplő számok a 31 kivételével nem osztói 5394-nek. A 31-hez tartozó
oszlopokban szereplő számok a 31 kivételével nem osztói 5394-nek. A 31-hez tartozó ![]() és
és ![]() számot pedig már megtaláltuk. Tehát három olyan
számot pedig már megtaláltuk. Tehát három olyan ![]() szám van, amelyre
szám van, amelyre ![]() .
.
Mi a helyzet nagyobb ![]() értékek esetén?
értékek esetén?
A ![]() értékek
értékek ![]() esetén gyorsan növekednek, ezért ezek lehetséges értékeinek száma nem túl nagy. Ezekkel osztva
esetén gyorsan növekednek, ezért ezek lehetséges értékeinek száma nem túl nagy. Ezekkel osztva ![]() -t, el tudjuk dönteni, hogy az egyes prímek szerepelhetnek-e
-t, el tudjuk dönteni, hogy az egyes prímek szerepelhetnek-e ![]() -ben.
-ben.
![]() és
és ![]() esetén pedig ha
esetén pedig ha ![]() osztói
osztói ![]() -gyel, illetve
-gyel, illetve ![]() egyenlők, a kapott egyenletek adnak lehetséges
egyenlők, a kapott egyenletek adnak lehetséges ![]() értékeket. Ha
értékeket. Ha ![]() nem prím, akkor a legkisebb prímosztója,
nem prím, akkor a legkisebb prímosztója, ![]() . Ha például
. Ha például ![]() 24-jegyű, akkor egy jó prímszámtáblázattal és programmal a
24-jegyű, akkor egy jó prímszámtáblázattal és programmal a ![]() -nél nem nagyobb
-nél nem nagyobb ![]() prímosztót viszonylag gyorsan, néhány perc alatt meg lehet találni.
prímosztót viszonylag gyorsan, néhány perc alatt meg lehet találni.
Egy kézenfekvő módosítás. Jelöljük ![]() -nel az
-nel az ![]() szám nála kisebb osztóinak összegét:
szám nála kisebb osztóinak összegét: ![]() .
.
Hogyan határozhatjuk meg ![]() ismeretében az
ismeretében az ![]() számot?
számot?
Az ![]() függvény nem alakítható szorzattá, ezért a
függvény nem alakítható szorzattá, ezért a ![]() -nél használtakhoz hasonló eljárások nem alkalmazhatók. Nem tudjuk a fentihez hasonló módszerrel eldönteni
-nél használtakhoz hasonló eljárások nem alkalmazhatók. Nem tudjuk a fentihez hasonló módszerrel eldönteni ![]() értékének ismeretében, hogy egy prím szerepel-e
értékének ismeretében, hogy egy prím szerepel-e ![]() -ben vagy nem.
-ben vagy nem.
Nem látszik jobb módszer, mint végigpróbálni minden lehetséges ![]() -t, hogy az adott
-t, hogy az adott ![]() tartozik-e hozzá.
tartozik-e hozzá.
Egy adott ![]() esetén milyen határok között kereshetjük
esetén milyen határok között kereshetjük ![]() értékét?
értékét?
Ha ![]() prím, akkor
prím, akkor ![]() , és fordítva.
, és fordítva.
Ha ![]() , ahol
, ahol ![]() prím, akkor
prím, akkor ![]() . A két egyenletből:
. A két egyenletből: ![]() . Tehát egy adott
. Tehát egy adott ![]() érték esetén
érték esetén ![]() , és ez a felső határ el is érhető.
, és ez a felső határ el is érhető.
Ez például azt jelenti, hogy egy 25-jegyű ![]() esetén
esetén ![]() nem lehet nagyobb 50-jegyűnél.
nem lehet nagyobb 50-jegyűnél.
Ha az 50-jegyűekig minden ![]() -t végig kellene próbálni, hogy az adott
-t végig kellene próbálni, hogy az adott ![]() érték tartozik-e hozzá, akkor ez igen sokáig tartana. Ha például egy számítógép minden
érték tartozik-e hozzá, akkor ez igen sokáig tartana. Ha például egy számítógép minden ![]() esetén átlagosan
esetén átlagosan ![]() s alatt döntené el, hogy hozzá az adott
s alatt döntené el, hogy hozzá az adott ![]() tartozik-e, akkor ez kb.
tartozik-e, akkor ez kb. ![]() évig tartana.
évig tartana.
Természetesen a próbálkozások száma csökkenthető. Például beláthatjuk, hogy
ha ![]() páros, akkor
páros, akkor
— ![]() páros, és van olyan
páros, és van olyan ![]() prímtényezője, amely páratlan kitevővel szerepel; vagy
prímtényezője, amely páratlan kitevővel szerepel; vagy
— ![]() páratlan négyzetszám;
páratlan négyzetszám;
ha ![]() páratlan, akkor
páratlan, akkor
— ![]() páros és minden
páros és minden ![]() prímtényezője páros kitevővel szerepel; vagy
prímtényezője páros kitevővel szerepel; vagy
— ![]() páratlan és van olyan
páratlan és van olyan ![]() prímtényezője, amely páratlan kitevővel szerepel.
prímtényezője, amely páratlan kitevővel szerepel.
Ez kb. felére csökkenti a próbálkozások számát.
Vizsgálhatjuk külön azon eseteket, amelyeknél egy adott ![]() -hez nagyon nagy
-hez nagyon nagy ![]() tartozik
tartozik
Már láttuk, hogy ha ![]() , ahol
, ahol ![]() prím, akkor
prím, akkor ![]() . Ez csak egyetlen próbálkozás.
. Ez csak egyetlen próbálkozás.
Ha ![]() , ahol
, ahol ![]() és
és ![]() prímek, akkor
prímek, akkor ![]() .
.
![]() . Ebből
. Ebből ![]() .
.
Ez már negyedrészére csökkenti a vizsgálandó intervallumot.
Mindezek a korlátozások azonban alig csökkentik a próbálkozások számát, és a szükséges időt.
Ha egy 25-jegyű ![]() -nél az 50-jegyűekig minden
-nél az 50-jegyűekig minden ![]() végigpróbálása helyett
végigpróbálása helyett
— a fent említettnél ![]() -szor gyorsabb gépekkel,
-szor gyorsabb gépekkel,
— és olyan meggondolásokat alkalmazva, keresnénk, amelynél ![]() számból csak 1-et kellene megnézni, már „csak”
számból csak 1-et kellene megnézni, már „csak” ![]() évig tartana.
évig tartana.
Láthatjuk, hogy egy nagyon kézenfekvő kis módosítás: ![]() helyett
helyett ![]() -ből határozzuk meg
-ből határozzuk meg ![]() értékét; néhány perc alatt megoldható feladatból belátható idő alatt megoldhatatlan problémát hoz létre.
értékét; néhány perc alatt megoldható feladatból belátható idő alatt megoldhatatlan problémát hoz létre.
(A ![]() -ből meghatározni
-ből meghatározni ![]() értékét feladat is exponenciális idejű probléma, de kb.
értékét feladat is exponenciális idejű probléma, de kb. ![]() -
-![]() -jegyű
-jegyű ![]() -ekig ez jó géppel és jó programmal már valóban néhány perc alatt megoldható.)
-ekig ez jó géppel és jó programmal már valóban néhány perc alatt megoldható.)
V. Milyen alkalmazásai lehetnek a megoldott problémának?
Ne csak az emelt szintű szóbelire való készülésnél, hanem folyamatosan, elméleti anyagnál is és feladatoknál is tegyük fel a kérdést: Mire lehet használni a tárgyalt ismeretet?
A követezőkben a IV/5. feladat módosításánál kapott eredmény felhasználását mutatjuk be.
Ha egy eljárás, algoritmus egyik irányban viszonylag gyorsan, fordított irányban viszont sokkal hosszabb idő alatt hajtható végre, akkor gondolhatunk annak titkosításban való alkalmazására.
Például két nagy prímszám összeszorzása egy számítógéppel gyorsan végrehajtható, de a szorzatból a két nagy prím visszakeresésére nem ismerünk rövid idő alatt elvégezhető eljárást. Ezen alapul az 1976-ban kifejlesztett RSA titkosítási módszer.
Jelenleg számítógépekkel egy kb. 25-30-jegyű ![]() szám nála kisebb osztói
szám nála kisebb osztói ![]() összegének meghatározása rövid idő, legfeljebb néhány perc alatt elvégezhető, de a IV/5. feladat módosításánál megállapítottuk, hogy hasonló hosszúságú
összegének meghatározása rövid idő, legfeljebb néhány perc alatt elvégezhető, de a IV/5. feladat módosításánál megállapítottuk, hogy hasonló hosszúságú ![]() -ből
-ből ![]() visszakeresésére belátható idejű módszert nem ismerünk. Tanítványaimmal ennek a ténynek a felhasználásával alakítottunk ki egy egyirányú titkosítási módszert.
visszakeresésére belátható idejű módszert nem ismerünk. Tanítványaimmal ennek a ténynek a felhasználásával alakítottunk ki egy egyirányú titkosítási módszert.
Az egyirányú titkosítás lényege az, hogy egy üzenetet akarunk úgy elküldeni, hogy aki kapja, az a megérkezéskor még ne tudja elolvasni, csak egy lenyomatot kapjon róla. később viszont, amikor elküldjük a valódi üzenetet, akkor a lenyomat alapján ellenőrizni tudja, hogy ugyanaz volt-e az első küldemény.
Egy példa. Ketten interneten sakkoznak, de a játszmát félbe kell szakítani és például másnap folytatják. Normál versenyen ilyenkor a lépésre következő megteszi a következő lépést, de ezt nem mondja meg a partnernek, hanem egy borítékba zárva leadja a versenybírónak. Ezt igazságosnak tartjuk, mert aki lépett, az tudja ugyan a lépést, de ha a szünet alatt találna is helyette jobbat, már nem változtathat. Hogyan lehet borítékolni a lépést internetes sakkozásnál, ha nincs versenybíró?
Nem a lépést, hanem annak egy lenyomatát küldi el a játékos, és csak a folytatáskor küldi a lépést. A partner a lenyomat alján ellenőrzi, hogy valóban ez volt-e a lépés. A sakklépés ASCII kódja egy ![]() szám, de nem ezt küldjük el (mert ebből a partner visszafejthetné a lépést), hanem a hozzá tartozó
szám, de nem ezt küldjük el (mert ebből a partner visszafejthetné a lépést), hanem a hozzá tartozó ![]() értéket. Mint korábban láttuk, egy elég nagy
értéket. Mint korábban láttuk, egy elég nagy ![]() -ből véges idő alatt nem tudja visszafejteni a partner az
-ből véges idő alatt nem tudja visszafejteni a partner az ![]() értéket. A sakklépéshez kicsi
értéket. A sakklépéshez kicsi ![]() szám, és kicsi
szám, és kicsi ![]() tartozna, ezért a sakklépést egy hosszabb szövegbe pl. egy versidézetbe ágyazzuk. (Ezt az eljárást „sózás”-nak szokás nevezni.)
tartozna, ezért a sakklépést egy hosszabb szövegbe pl. egy versidézetbe ágyazzuk. (Ezt az eljárást „sózás”-nak szokás nevezni.)
Nézzünk erre egy konkrét példát! A borítékolt lépés, azaz a szöveg: Hc6-d4
ASCII kódja: ![]() ,
, ![]()
Bár ebből az ![]() -ből sem lenne könnyű visszafejteni
-ből sem lenne könnyű visszafejteni ![]() -t, de mégsem célszerű ezt elküldeni, mert a szóba jöhető lépések végigpróbálásával megtalálható ez az
-t, de mégsem célszerű ezt elküldeni, mert a szóba jöhető lépések végigpróbálásával megtalálható ez az ![]() . Mi a megoldás? Helyezzük el a lépést egy hosszabb szövegbe!
. Mi a megoldás? Helyezzük el a lépést egy hosszabb szövegbe!
Új szöveg: te édes Hc6-d4 mostoha
![]()
![]()
Ezt az 56-jegyű ![]() -t küldjük el, ebből a partnernek nincs esélye visszafejteni az eredeti szöveget. Látható, hogy az új
-t küldjük el, ebből a partnernek nincs esélye visszafejteni az eredeti szöveget. Látható, hogy az új ![]() számban megtalálható az eredeti
számban megtalálható az eredeti ![]() , de az új
, de az új ![]() -ben nyoma sincs az eredetinek.
-ben nyoma sincs az eredetinek.
Azért is jó ez a titkosítás, mert akár az eredeti, akár a bővített szöveg kis változtatása is teljesen megváltoztatja a lenyomatot. Változtassuk például a sakklépés H betűjét h-ra, ekkor az ![]() szám közepén a 072 szám 104-re változik, ez
szám közepén a 072 szám 104-re változik, ez ![]() -ben csak kis változás, de
-ben csak kis változás, de ![]() teljesen más lesz:
teljesen más lesz:
Módosított szöveg: te édes hc6-d4 mostoha
![]()
![]()
Miért tettük versidézetbe az üzenetet?
Egy adott ![]() értékhez több
értékhez több ![]() is tartozhat. Például
is tartozhat. Például ![]() , 3521, 5489, 9329, 11201, 14849 esetén is
, 3521, 5489, 9329, 11201, 14849 esetén is ![]() . Azért kell értelmes szöveget, irodalmi idézetet használni a sózáshoz, mert ha ezt nem kötnénk ki, akkor a lépést borítékoló játékosnak esetleg lehetősége volna megfelelően megválasztott „sózással” egy később talált, jobb lépéshez ugyanazt a lenyomatot előállítani. Irodalmi idézet használata esetén viszont teljesen minimális annak a valószínűsége, hogy ugyanazon
. Azért kell értelmes szöveget, irodalmi idézetet használni a sózáshoz, mert ha ezt nem kötnénk ki, akkor a lépést borítékoló játékosnak esetleg lehetősége volna megfelelően megválasztott „sózással” egy később talált, jobb lépéshez ugyanazt a lenyomatot előállítani. Irodalmi idézet használata esetén viszont teljesen minimális annak a valószínűsége, hogy ugyanazon ![]() -hez két irodalmi idézetbe ágyazott sakklépés tartozzon.
-hez két irodalmi idézetbe ágyazott sakklépés tartozzon.
Az egyirányú kódolásnak sokfélé felhasználása lehetséges. Ezekből csak néhányat említünk.
— Ha egy munkára árajánlatot akarunk adni, és el akarjuk kerülni annak a lehetőségét is, hogy a borítékba zárt ajánlatunkat idő előtt megnézze valaki, és azt közölje a konkurenciával, akkor a fenti módszerrel küldhetjük el az ajánlatot: Szöveg: 32 millió Ft Hozz reá víg esztendőt
![]() = 39 801 904 735 194 256 535 843 329 980 775 011 282 180 576 600 895 974 789 714 855 418 597 707 148 511 355 857 326 363 050 770 274 141 360 164
= 39 801 904 735 194 256 535 843 329 980 775 011 282 180 576 600 895 974 789 714 855 418 597 707 148 511 355 857 326 363 050 770 274 141 360 164
Ezt küldjük el. Ebből az eredeti ajánlat nem fejthető vissza. Borítékbontásnál megadjuk az eredeti üzenetet, és ellenőrizhető, hogy valóban ez az ![]() tartozik hozzá.
tartozik hozzá.
— Ha valamilyen információhoz, rendszerhez jelszóval férhetünk hozzá, akkor a jelszavainkat (elvileg) nem szabad tárolni, hanem csak azoknak egy lenyomatát, amelyből nem fejthető vissza a jelszó. A jelszóból képezzük az ![]() számot, a lenyomat legyen az
számot, a lenyomat legyen az ![]() .
.
— Elképzelhető műszaki alkalmazás is. Ha gépkocsinkat távirányítóval nyitjuk, akkor a távirányító jelét le lehet hallgatni, és a lehallgatott jellel már más is tudja nyitni az autót. Kiküszöbölhető ez például úgy, hogy az autót minden zárásnál egy máik ![]() -nel zárjuk, (ezt lehallgathatják,) és a hozzá tartozó
-nel zárjuk, (ezt lehallgathatják,) és a hozzá tartozó ![]() -nel nyitjuk.
-nel nyitjuk. ![]() -ből
-ből ![]() nem határozható meg.
nem határozható meg.
Több kérdés is felvetődhet ennél a titkosítási módszernél. Csak néhányat említünk. Mit tehetünk, ha az üzenet hosszú, és a nagy ![]() számnak nem lehet rövid idő alatt kiszámítni az
számnak nem lehet rövid idő alatt kiszámítni az ![]() -jét. (Ez esetben az üzenetet megfelelő hosszúságú darabokra bontjuk.) Mit tehetünk, ha az üzenetből kapott
-jét. (Ez esetben az üzenetet megfelelő hosszúságú darabokra bontjuk.) Mit tehetünk, ha az üzenetből kapott ![]() szám prím, vagy valamilyen könnyen visszafejthető
szám prím, vagy valamilyen könnyen visszafejthető ![]() -t kapunk? Ezekre, és további a problémákra több év alatt tanítványaimmal, Freud Róbertnek, az ELTE TTK Algebra és Számelmélet Tanszék tanárának segítségével megkerestük a megoldásokat.
-t kapunk? Ezekre, és további a problémákra több év alatt tanítványaimmal, Freud Róbertnek, az ELTE TTK Algebra és Számelmélet Tanszék tanárának segítségével megkerestük a megoldásokat.
Ezzel a kutatással tanítványaim több hazai innovációs versenyen lettek díjazottak, és ketten 2012-ben Pittsburgh-ben, az ISES nemzetközi tudományos és innovációs versenyen 4. helyezést értek el.
A kutatás ismertetője, a résztvevő tanítványaim neve és egy program, amellyel bárki küldhet tikosított üzenetet, megtalálható iskolánk honlapján a következő címen:
http://www.bomateka.hu/pseg-matek/index.htm
Kiindulási feladatunk az volt, hogy ![]() -ből határozzuk meg
-ből határozzuk meg ![]() értékét. A módosítás:
értékét. A módosítás: ![]() -ből határozzuk meg
-ből határozzuk meg ![]() értékét. A további kérdés: milyen alkalmazása lehet ennek az egyik irányban viszonylag gyors, másik irányban sokkal lassúbb eljárásnak? Az eredeti feladat továbbgondolása, a tanulók számára sikereket hozó alkalmazáshoz, kutatáshoz vezetett. Cikkünk korábbi részeiben felvetett kérdések is, ez a részletesen bemutatott alkalmazás pedig különösen jól mutatják: hasznos az, ha tanítványainkat rászoktatjuk, hogy egy feladat megoldása után még próbálják továbbgondolni a dolgot, tegyenek fel újabb kérdéseket.
értékét. A további kérdés: milyen alkalmazása lehet ennek az egyik irányban viszonylag gyors, másik irányban sokkal lassúbb eljárásnak? Az eredeti feladat továbbgondolása, a tanulók számára sikereket hozó alkalmazáshoz, kutatáshoz vezetett. Cikkünk korábbi részeiben felvetett kérdések is, ez a részletesen bemutatott alkalmazás pedig különösen jól mutatják: hasznos az, ha tanítványainkat rászoktatjuk, hogy egy feladat megoldása után még próbálják továbbgondolni a dolgot, tegyenek fel újabb kérdéseket.
Katz Sándor
a Bonyhádi Petőfi Sándor Evangélikus Gimnázium és az Erdős Pál Tehetséggondozó Iskola tanára
Irodalomjegyzék
- 5
- Gyapjas Ferenc, Reiman István: Elemi matematika feladatgyűjtemény I., (ELTE jegyzet) Nemzeti Tankönyvkiadó 1993.
- 6
- Katz Sándor: Játékos matematika, Zalai Matematikai Tehetségekért Alapítvány 2016.
- 7
- Erdős Pál—Surányi János: Válogatott fejezetek a számelméletből, Poligon Könyvtár 1996.
- 8
- K. Guy Richard: Unsolved Problems in Number Theory, Springer, 2004.
- 9
- Pál Erdős: Über die Zahlen der Form
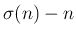 und
und 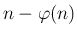 , Elemente der Mathematik 1973. 83—87. oldal
, Elemente der Mathematik 1973. 83—87. oldal









