Egy feladat és ami róla az eszembe jutott...
A mai számban egy geometriai feladatot járunk körbe, amelyet Laczkó László kollégám dolgozott fel. Az anyag megtalálható a Budapesti Fazekas Gimnázium matematikaoktatási portálján (http://matek.fazekas.hu) a cikkek között, „Ismételjük a geometriát egy feladaton keresztül!” címmel. A cikk címe nagyon találó, pont ez van a cikk készítésének ötlete mögött. Az ott szereplő megoldások közül válogatok és mutatok meg néhányat.
A feladat
Az 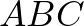 hegyesszögű háromszög
hegyesszögű háromszög  -nél levő szöge
-nél levő szöge 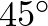 .
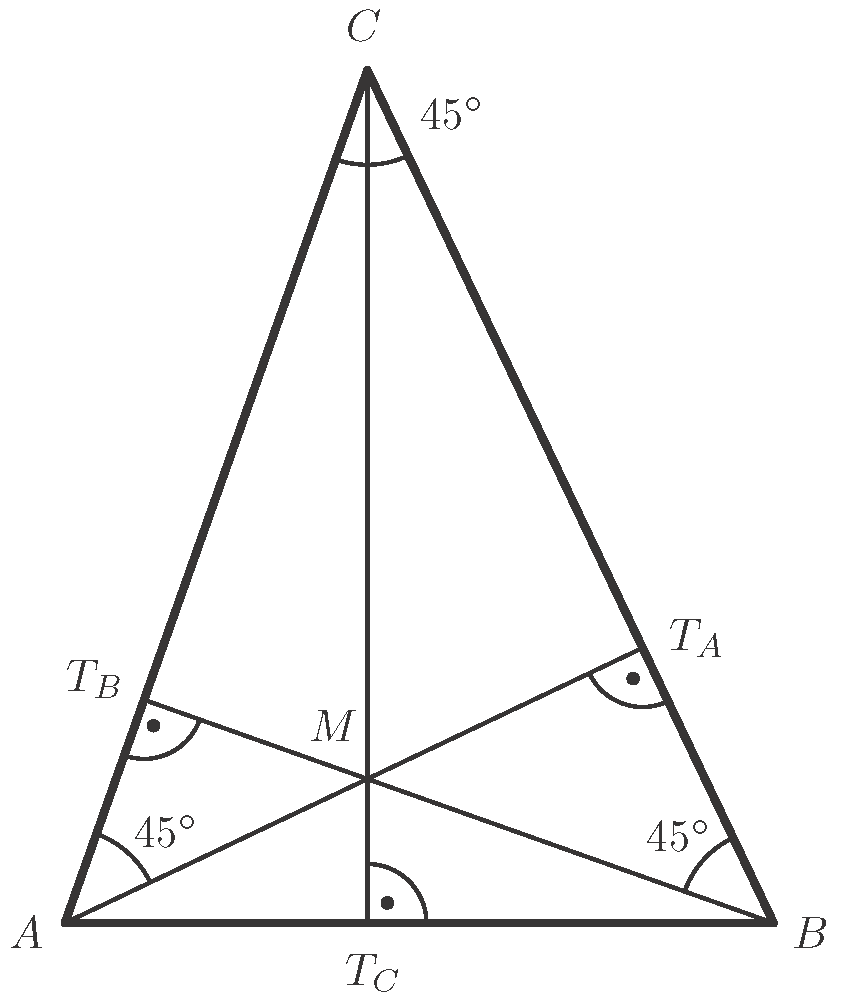
. 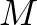 a háromszög magasságpontja. Bizonyítsuk be, hogy
a háromszög magasságpontja. Bizonyítsuk be, hogy 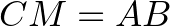 !
!
1. megoldás
Használjuk az ábra jelöléseit!
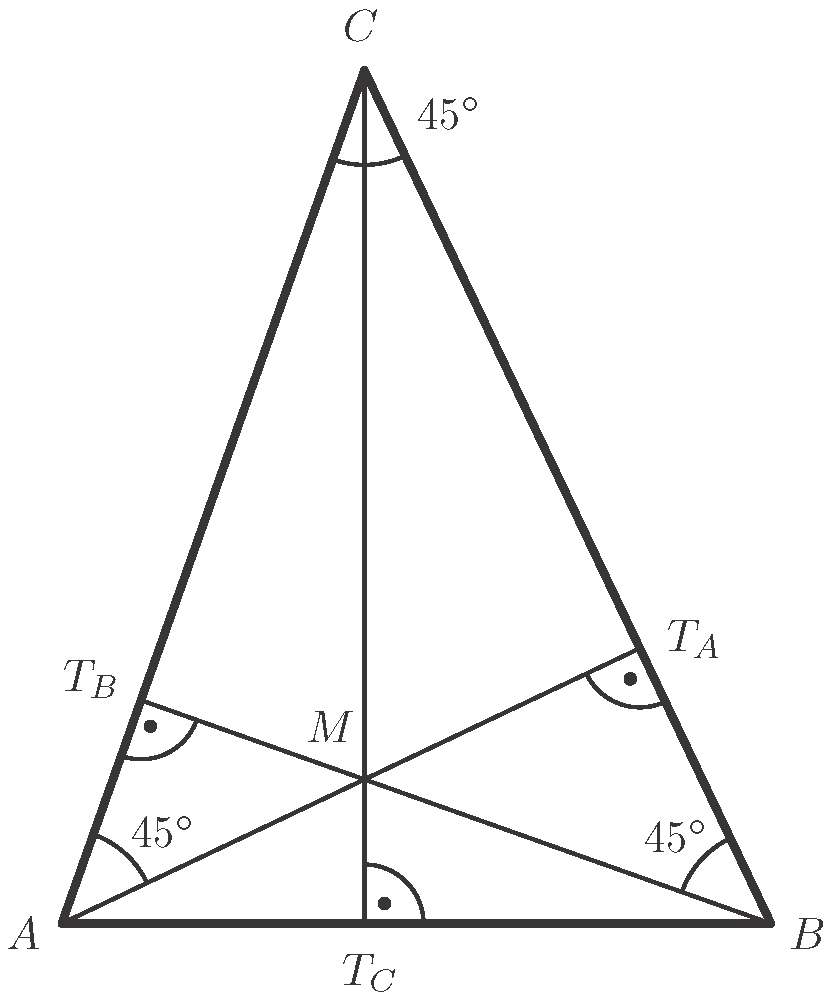
A 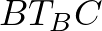 háromszög derékszögű és egyenlő szárú, hiszen
háromszög derékszögű és egyenlő szárú, hiszen
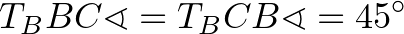 .
.Ezért
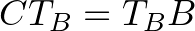 .
.Az 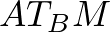 háromszög is derékszögű és egyenlő szárú, hiszen
háromszög is derékszögű és egyenlő szárú, hiszen
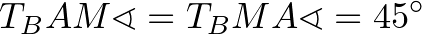 .
.Ezért
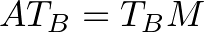 .
.A 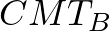 és
és 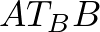 háromszögek egybevágók, mert két-két oldaluk (
háromszögek egybevágók, mert két-két oldaluk (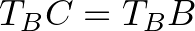 és
és 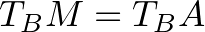 ) és közbezárt szögük egyenlő (
) és közbezárt szögük egyenlő (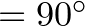 ).
).
Ezért a harmadik oldaluk is megegyezik, azaz
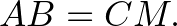
2. megoldás
Használjuk az ábra jelöléseit!
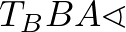 és
és 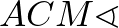 merőleges szárú hegyesszögek, ezért
merőleges szárú hegyesszögek, ezért
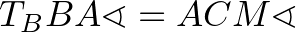 .
.Az 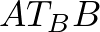 és
és 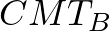 háromszögek derékszögűek.
háromszögek derékszögűek.
A 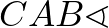 szög (és a derékszög) közös ebben a két háromszögben, tehát hasonlóak.
szög (és a derékszög) közös ebben a két háromszögben, tehát hasonlóak.
A 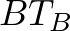 és
és 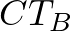 egymásnak megfelelő oldalak egyenlőek, mert a
egymásnak megfelelő oldalak egyenlőek, mert a 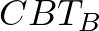 háromszög egyenlő szárú derékszögű (1. megoldás) ezért a két háromszög egybevágó, azaz
háromszög egyenlő szárú derékszögű (1. megoldás) ezért a két háromszög egybevágó, azaz
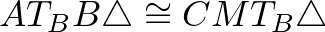 .
.Ebből következik, hogy minden megfelelő oldal egyenlő, azaz
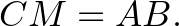
3. megoldás
Használjuk az ábra jelöléseit!
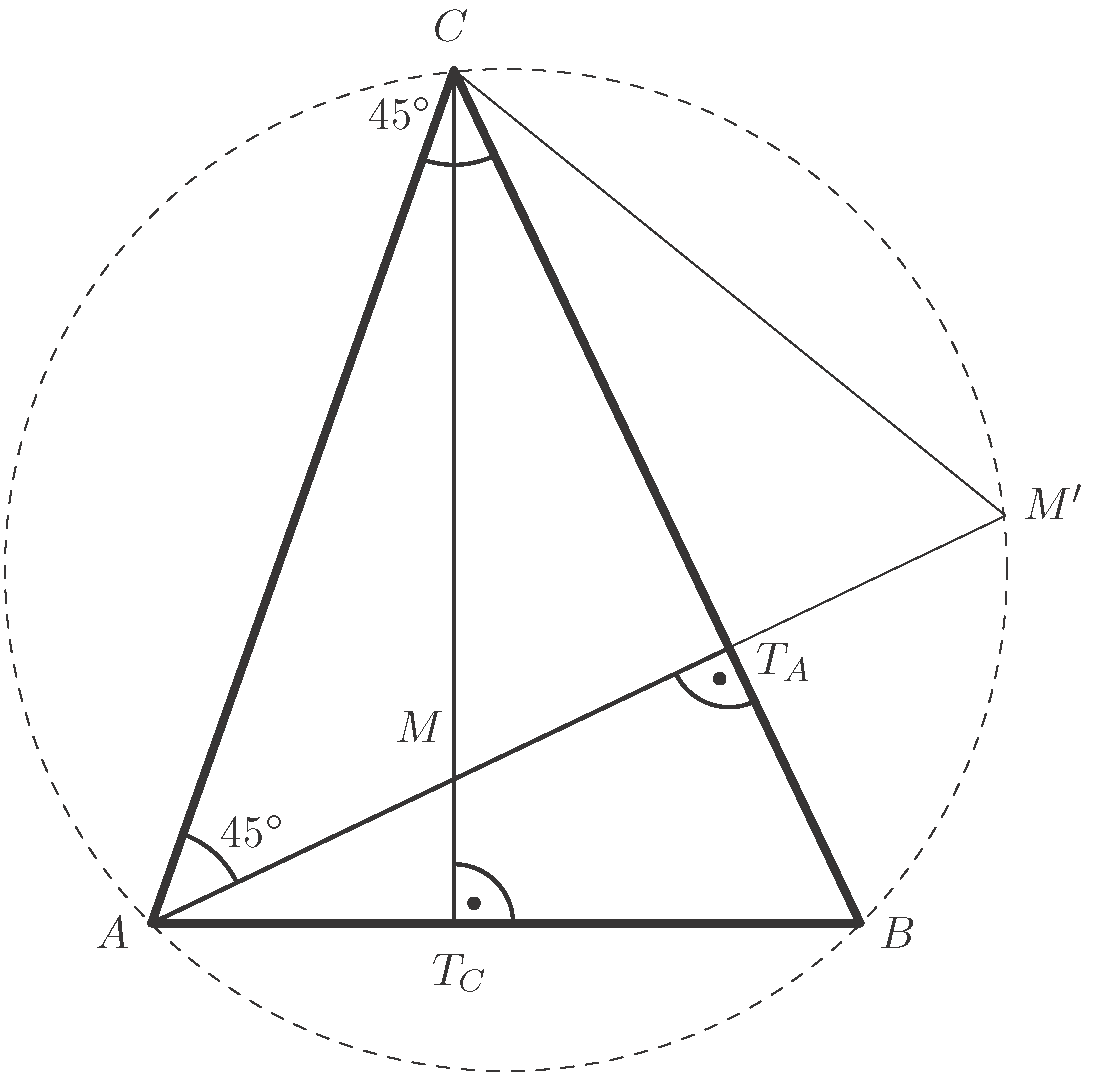
Tükrözzük tengelyesen az 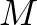 pontot a
pontot a 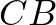 oldalra, a tükörképet
oldalra, a tükörképet 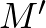 jelöli.
jelöli.
Ismeretes, hogy a magasságpontot az oldalra tengelyesen tükrözve a tükörkép (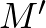 ) pont a háromszög köré írt körön van.
) pont a háromszög köré írt körön van.
A tükrözés miatt
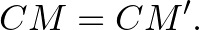
Ugyanakkor
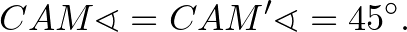
Az 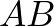 és
és 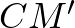 húrok ugyanabban a körben vannak és mind a kettőhöz
húrok ugyanabban a körben vannak és mind a kettőhöz 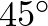 -os kerületi szög tartozik, tehát
-os kerületi szög tartozik, tehát
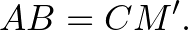
Mivel 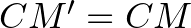 , így
, így
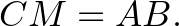
4. megoldás
Használjuk az ábra jelöléseit!
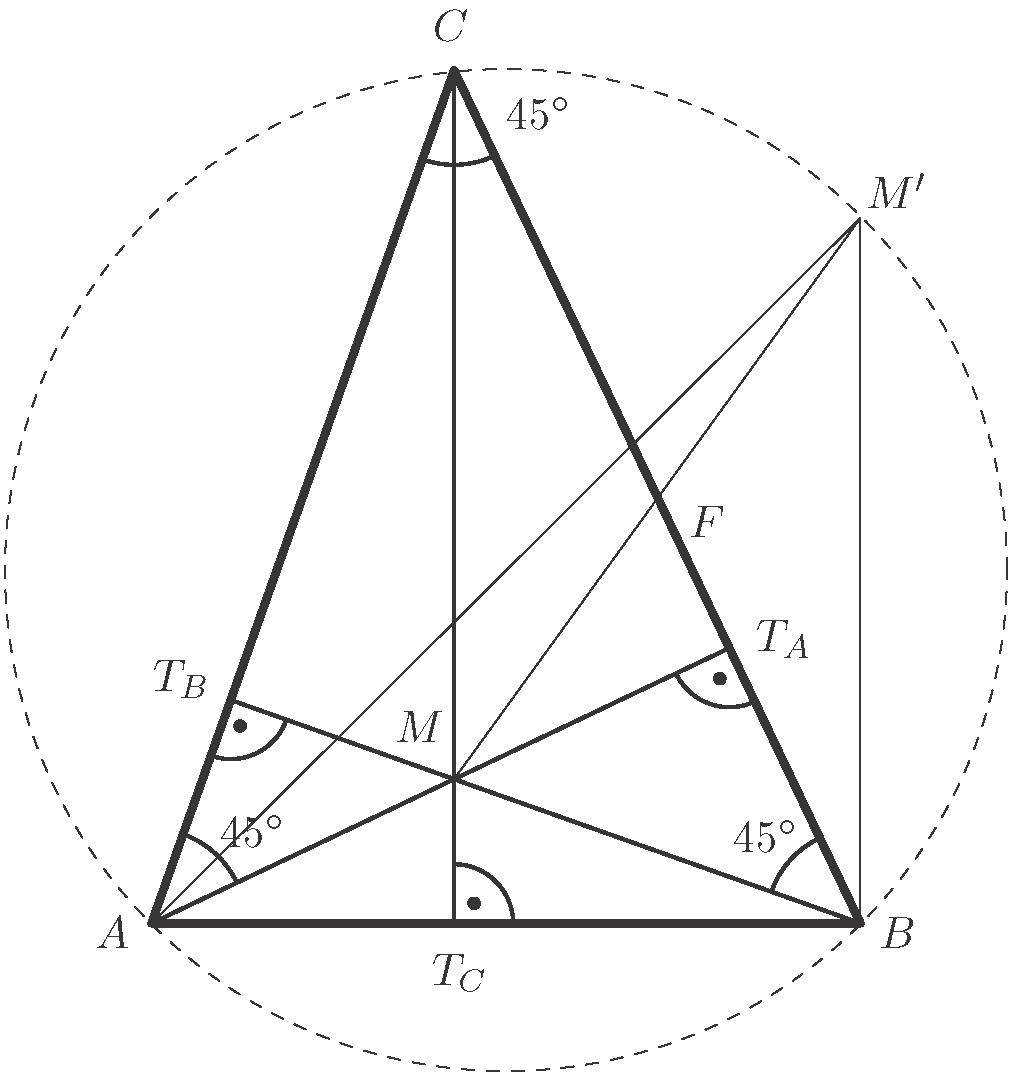
A 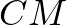 szakaszt
szakaszt 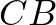 oldal felezőpontjára (
oldal felezőpontjára (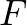 ) tükrözve kapjuk
) tükrözve kapjuk 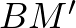 -t. Ismeretes, hogy
-t. Ismeretes, hogy 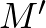 a körülírt körön van.
a körülírt körön van.
A középpontosan tükrözött szakasz párhuzamos a képével. A 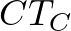 magasság merőleges az
magasság merőleges az 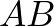 alapra, tehát
alapra, tehát
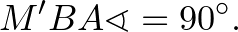
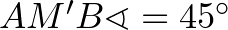 , mert az
, mert az 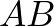 ívhez tartozó kerületi szög.
ívhez tartozó kerületi szög.
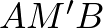 egyenlő szárú derékszögű háromszög, ezért
egyenlő szárú derékszögű háromszög, ezért
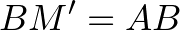 .
.A tükrözés miatt
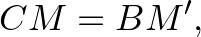
ezért
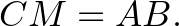
5. megoldás
Használjuk az ábra jelöléseit!
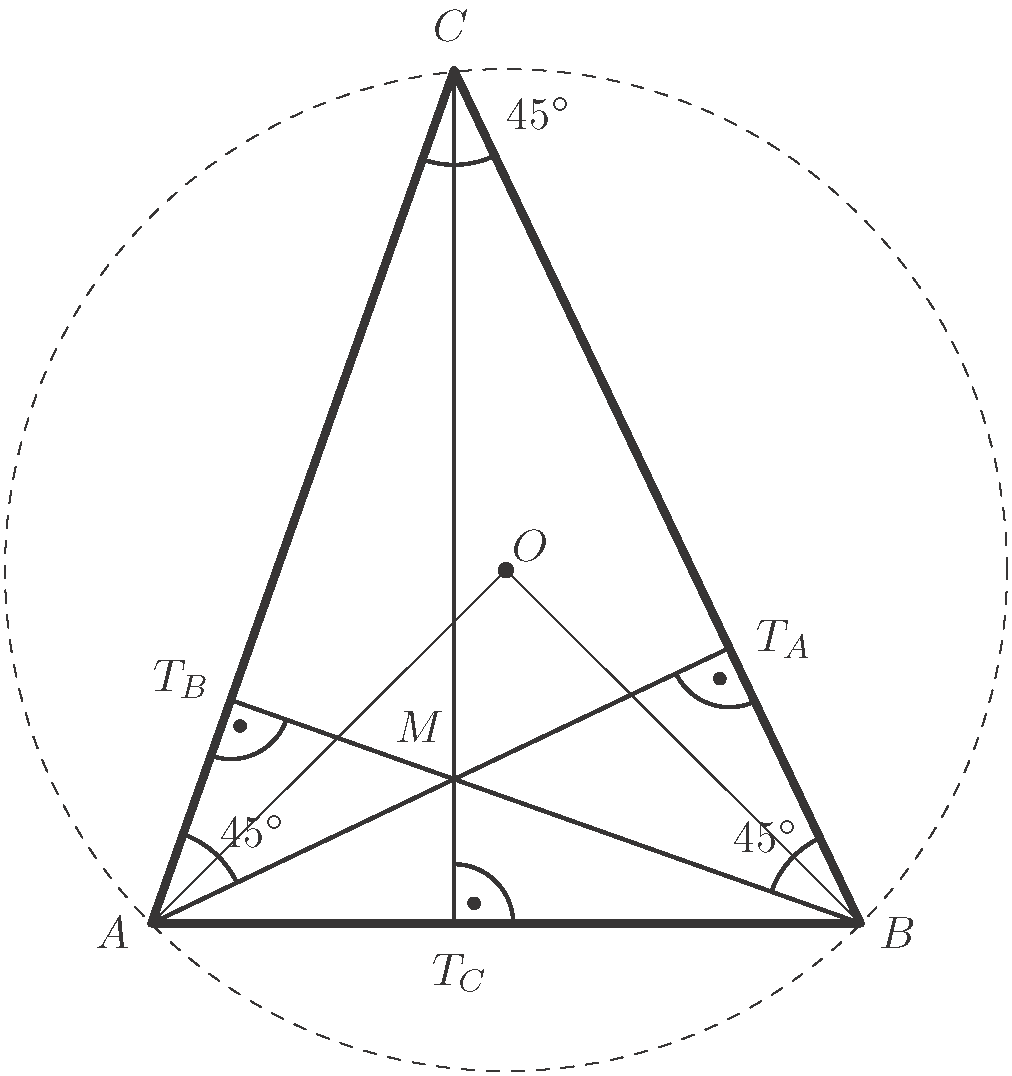
Legyen  a háromszög köré írható körének középpontja.
a háromszög köré írható körének középpontja.
Az 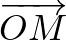 vektort jelölje
vektort jelölje 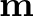 , az
, az 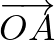 ,
, 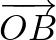 ,
, 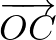 és
és 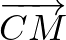 vektorokat rendre
vektorokat rendre 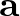 ,
, 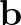 ,
, 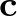 és
és 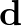 .
.
Felhasználjuk, hogy a magasságpontba mutató vektorra
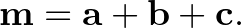
Ebből a 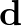 vektorra kapjuk, hogy
vektorra kapjuk, hogy

Az 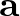 és
és 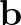 vektorok által kifeszített paralelogramma egyik átlója
vektorok által kifeszített paralelogramma egyik átlója 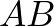 , a másik
, a másik 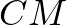 .
.
A kerületi és középponti szögek tétele miatt
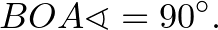
Így az 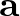 és
és 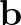 vektorok által kifeszített paralelogramma négyzet, mert az
vektorok által kifeszített paralelogramma négyzet, mert az 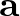 ,
, 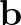 vektorok hossza a köré írt kör sugarával egyenlő.
vektorok hossza a köré írt kör sugarával egyenlő.
A négyzet átlói egyenlőek, így
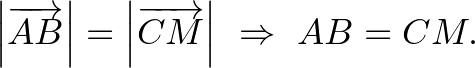
6. megoldás
Használjuk az ábra jelöléseit!
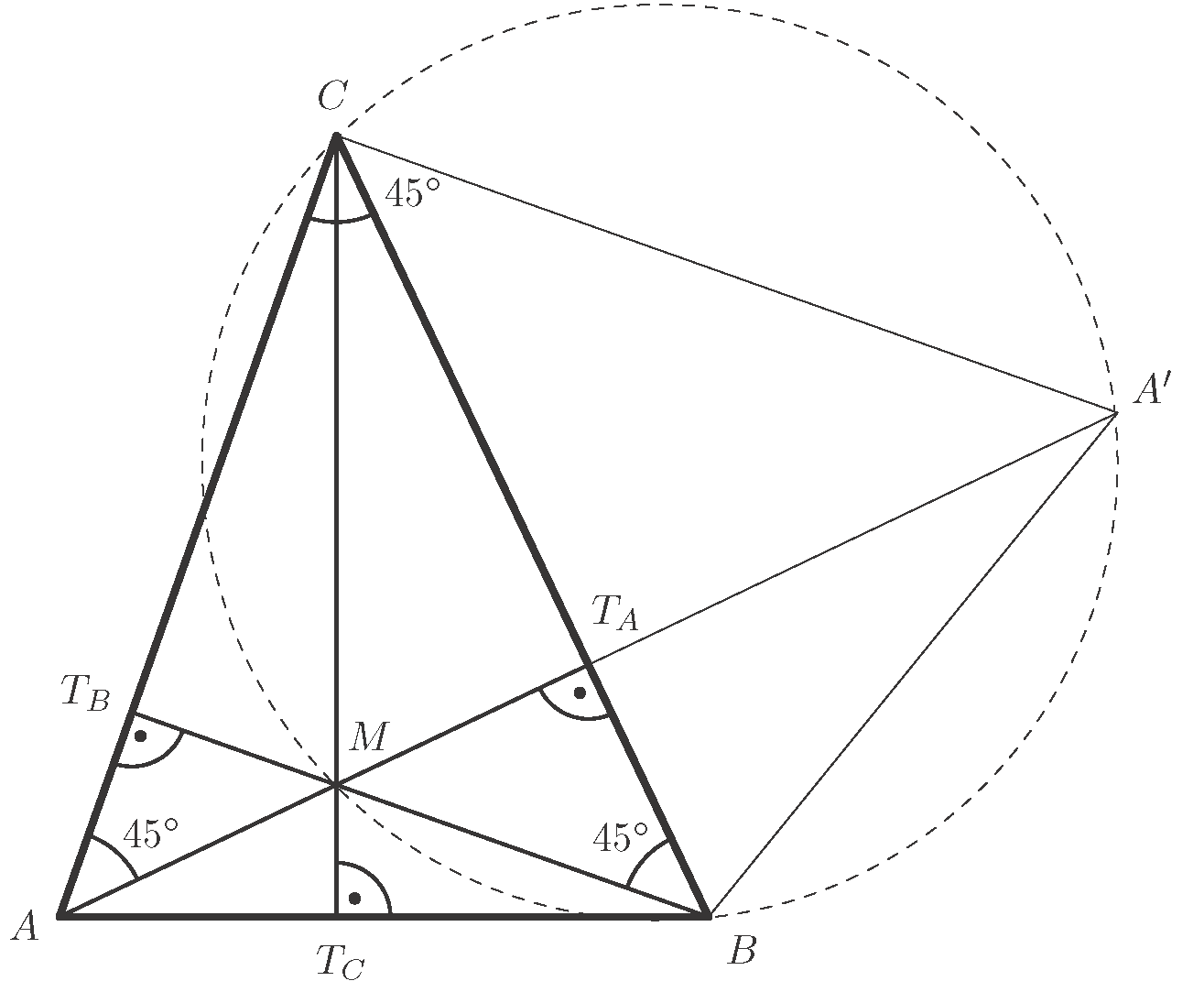
A 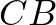 oldalra tükrözzük az
oldalra tükrözzük az 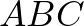 háromszöget,
háromszöget, 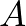 tükörképe legyen
tükörképe legyen 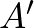 .
.
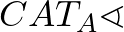 és a tükörképe,
és a tükörképe, 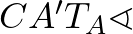 is
is 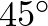 , valamint
, valamint 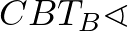 is annyi.
is annyi.
Ezért a 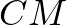 szakasz
szakasz 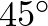 -os látókörén van
-os látókörén van 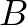 és
és 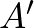 is.
is.
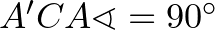 a tükrözés miatt, ezért
a tükrözés miatt, ezért 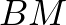 szakasz párhuzamos
szakasz párhuzamos 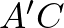 szakasszal, így
szakasszal, így 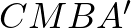 húrtrapéz, melynek szárai
húrtrapéz, melynek szárai 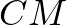 és
és 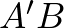 egyenlőek. Ezért
egyenlőek. Ezért
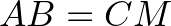 .
.
7. megoldás
Tegyük koordinátarendszerbe a feladatot úgy, hogy a  csúcs az origóba, az
csúcs az origóba, az 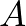 csúcs az
csúcs az 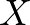 tengelyre essen. Használjuk az ábra jelöléseit!
tengelyre essen. Használjuk az ábra jelöléseit!
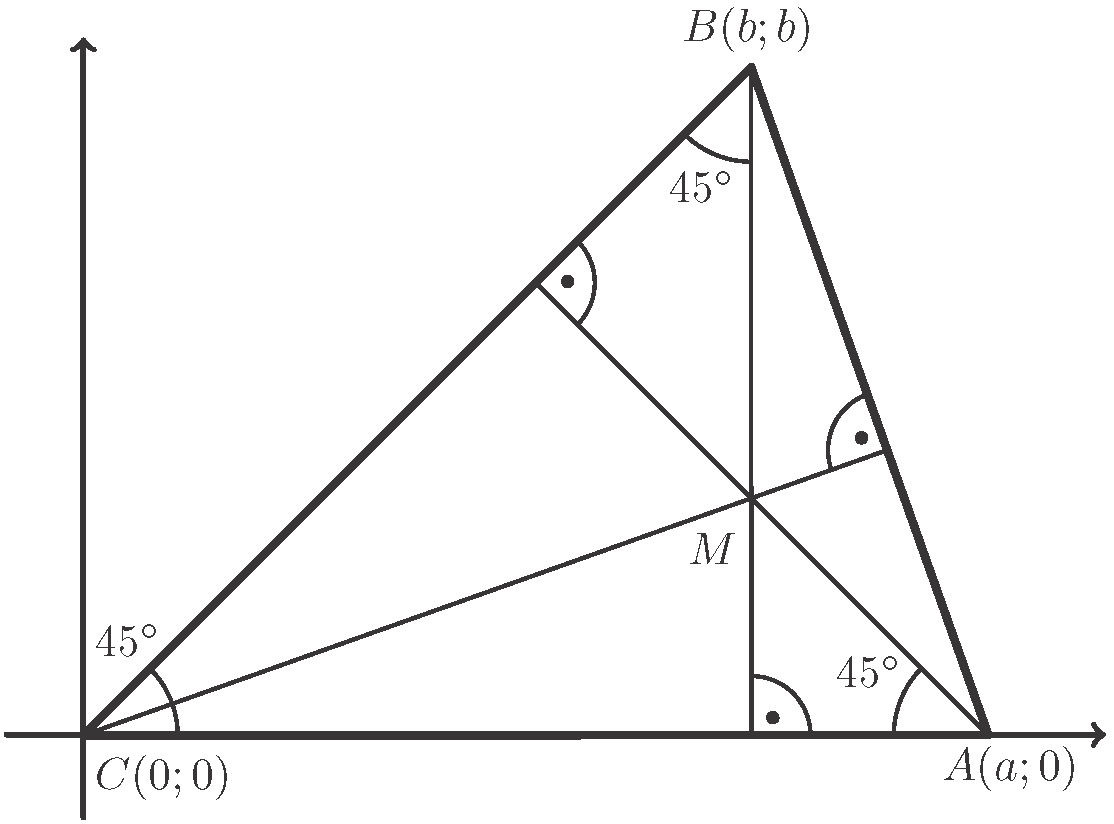
A csúcsok koordinátái:
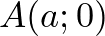 , hiszen az
, hiszen az 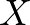 tengelyen van.
tengelyen van. 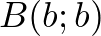 , hiszen az
, hiszen az 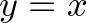 egyenes egy pontja.
egyenes egy pontja. 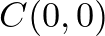 , hiszen az origóban van.
, hiszen az origóban van.
Az 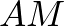 egyenes merőleges
egyenes merőleges 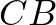 -re, aminek a meredeksége 1, ezért egyenlete
-re, aminek a meredeksége 1, ezért egyenlete
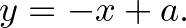
Az 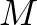 pont esetén
pont esetén  és innen az
és innen az 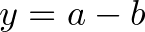 ,
, 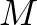 pont koordinátája
pont koordinátája
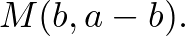
Az 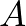 és
és 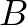 pontok távolsága
pontok távolsága
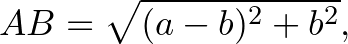
a  és
és 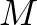 pontok távolsága
pontok távolsága
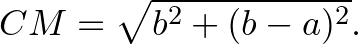
Látható, hogy
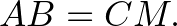
8. megoldás
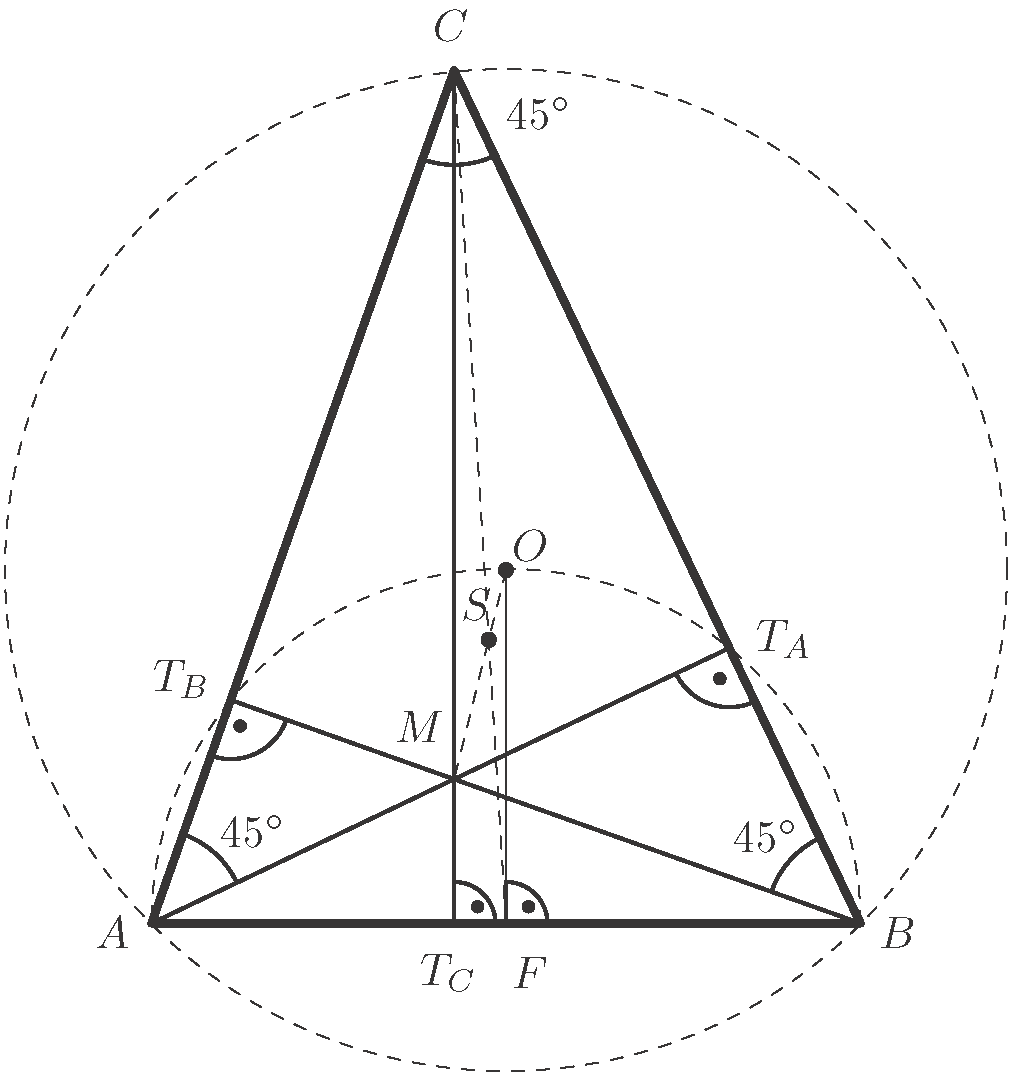
Legyen  a háromszög köré írható kör középpontja,
a háromszög köré írható kör középpontja, 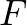 az
az 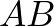 oldal felezőpontja,
oldal felezőpontja, 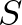 a háromszög súlypontja.
a háromszög súlypontja. 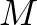 a háromszög magasságpontja.
a háromszög magasságpontja.
Tudjuk, hogy 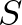 harmadolja az
harmadolja az 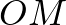 szakaszt, valamint
szakaszt, valamint 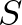 harmadolja a
harmadolja a 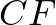 súlyvonalat.
súlyvonalat.
A kerületi és középponti szögek tétele miatt 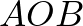 háromszög derékszögű és egyenlő szárú.
háromszög derékszögű és egyenlő szárú.
Mivel 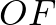 az
az 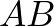 Thalész-körének sugara,
Thalész-körének sugara,
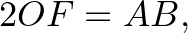
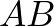 pedig az átmérője.
pedig az átmérője.
Tudjuk, hogy az 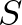 -re vonatkozó (
-re vonatkozó (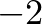 ) -szeres nagyítás az
) -szeres nagyítás az 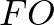 szakaszt a
szakaszt a 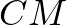 szakaszba viszi. Így
szakaszba viszi. Így
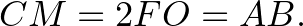
9. megoldás
Helyezzük el a háromszöget a Gauss-féle komplex számsíkon úgy, hogy a háromszög köré írt kör középpontja ( ) az origó legyen. Használjuk az ábra jelöléseit!
) az origó legyen. Használjuk az ábra jelöléseit!
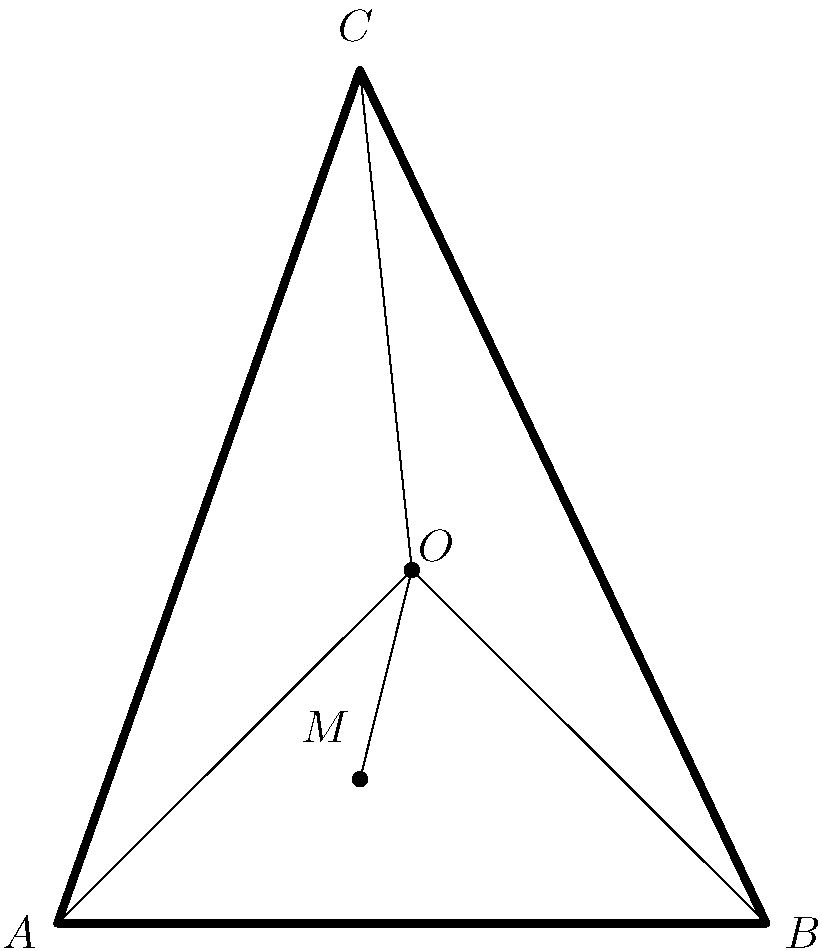
A kerületi és középponti szögek tétele miatt 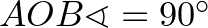 , és
, és 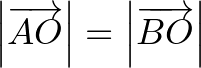 ezért
ezért
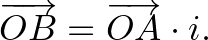
Ekkor
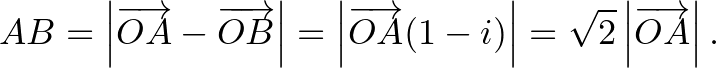
Ismert, hogy 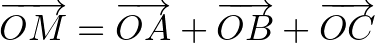 , így
, így
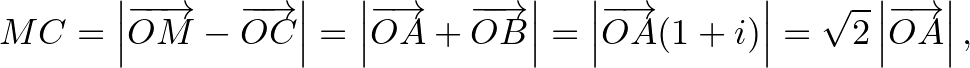
ami azt jelenti, hogy
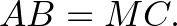
Visszacsatolás
Az Úton-módon 1. cikkében levő feladattal kapcsolatban ismét kaptam megoldásokat. Most Tatár Zsuzsanna Mária kolléganő írt 6 megoldást. A megoldások „nem vágnak teljesen bele” az eredeti elképzelésbe, hogy elemi megoldást adjunk a feladatra. Azért a küldött megoldások küzül – szubjektíven – egyet kiválasztottam, amit most megmutatok.
Tatár Zsuzsanna Mária, Esztergom megoldása
Tegyük koordinátarendszerbe az ábránkat! Az alapháromszög oldala legyen 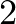 egység.
egység.
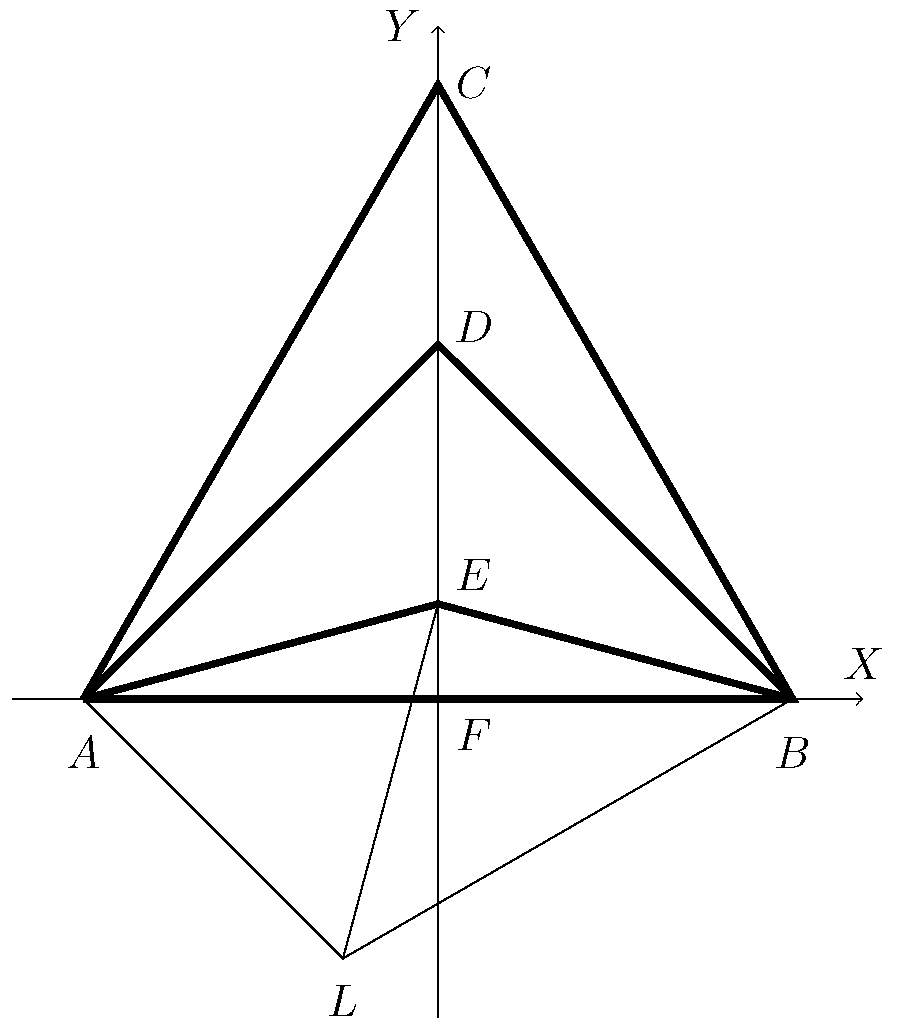
Ekkor a pontok koordinátái (rövid számolással adódnak):
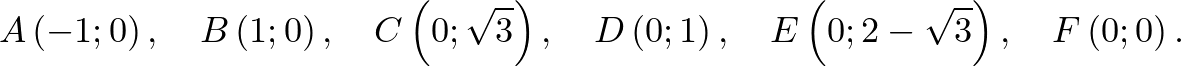
Forgassuk el az 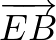 vektort 90 fokkal az óramutató járásával megegyező irányba. Így megkapjuk az
vektort 90 fokkal az óramutató járásával megegyező irányba. Így megkapjuk az 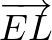 vektort.
vektort.
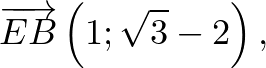

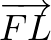 helyvektor végpontja megadja az
helyvektor végpontja megadja az 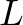 pont koordinátáit.
pont koordinátáit.
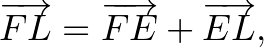
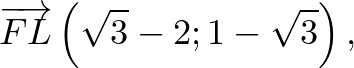
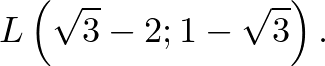
Tekintsük az 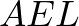 háromszög oldalainak hosszát:
háromszög oldalainak hosszát:
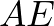 |
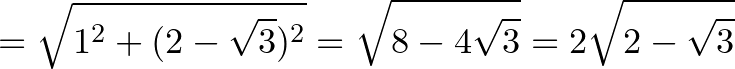 |
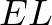 |
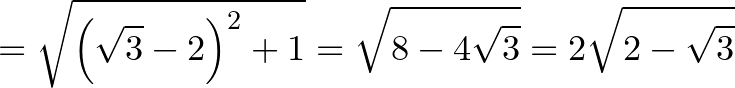 |
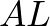 |
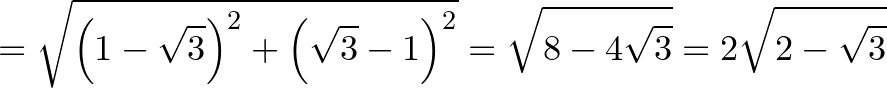 |
Tehát az 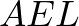 háromszög szabályos,
háromszög szabályos, 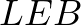 háromszög derékszögű.
háromszög derékszögű.
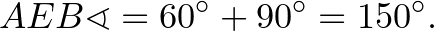
Zárszó
Kedves Olvasó! Ha egy másik „szép” megoldást talál, kérem küldje el nekem a Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát. e-mail címre. Ezeket az újabb megoldásokat összegyűjtve időnként (terveim szerint) szintén megmutatnám.
Megemlékezés
65 éves korában elhunyt Petz György szerkesztő, író, költő, tanár, a Szépírók Társasága tagja. A nyugdíjbavonulása előtti években a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium tanára volt, kollégámat tisztelhettem benne.
Miért írom mindezt?
Amikor e cikksorozatnak címet kerestem, hozzá fordultam ötletekért. Elmondtam neki, hogy mi lenne a cikkekben, hogyan is gondolom. Persze – akik ismerték, tudják róla, mindig viccelt – néhány tréfás megjegyzést tett némi mosoly kíséretében a felvetésre. Ám rövid időn belül sok javaslatot tett elém, végül is az „Úton–módon” cím nyert. Szóval e sorozat nevének ő volt az ötletgazdája. Emlékére írtam ezt a pár sort.









